小学校「福島県標準学力診断検査問題」による学力分析報告書1984-002/98page

標準偏差が10の正規分布を基準として決めておき、これにその得点の分布の同じ割合を対応させることによって得られたものである。
図1　得点と正規偏差値の変換

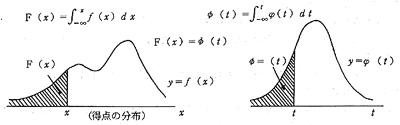(得点の分布)　　　　　(平均値50、標準偏差値10の正規分布)

得点x―正規偏差値t

正規偏差値は、得点の累積相対度数を求めるだけで表3から得られる。得点の分布がどんな分布であろうとも、それらをみな正規偏差値に変換しておけば、これらは、みな同一の基準分布に変換されているので、正規偏差値どうしの比較は、すべて同一の分布の上でなされることになり正確に比較できる。
一般に、標準点としては、いわゆる偏差値が用いられるのであるが、本検査において、この偏差値を採用しなかった理由は次の通りである。
偏差値が意味をもつのは、得点の分布が正規分布をする時で、この時のみ、偏差値は集団の中での相対的な自分の位置を表1、表2のように明示する。
表1　得点の分布が正規分布をするときの偏差値区分

偏差値	20	25	30	35	40	45	50	55	60	65	70	75	80
上からの%	99.9	99.4	98	93	84	69	50	31	16	7	2	0.6	0.14

　

表2　得点の分布が正規分布をするときの偏差値区分 偏差値 〜37 38〜54 55〜 3段階(%) 1　(10) 2　(60) 3　(30)	偏差値 〜34 35〜44 45〜54 55〜64 65〜 5段階(%) 1　(7) 2　(24) 3　(38) 4　(24) 5　(7)
(1、2年用)	(3、4、5、6年用)

ところで、一般に検査の成績はなかなか正規分布をするものではない。
得点の分布が正規分布をしないときは、偏差値は集団の中での自分の相対的な位置を明示しないから、他教科間のそれぞれの偏差値を比較しても、どちらがその集団の中で良いのか、わるいのかは比較できない。(標準テストと称しているものの中には、得点の分布の正規性も検討せず標準点として偏差値を用いているものもあるが、これは正しくない。)
それでは、得点の分布が正規分布をしていない場合でも、得点を変換した値が、集団の中の相対的な位置を明示するようなものはないか。このような要求のもとに考えられた変換が図1の変換であり、この変換によって得られた得点が正規偏差値(T得点)なのである。