尋媶婭梫戞6崋 妛廗巜摫夵慞偵娭偡傞尋媶 棟壢幚尡 - 030/036page
壒尮幵偺懍搙u偲丆婰榐巻忋偵夋偐傟偨攇偺攇挿兩偲偺娭學傪帵偟偨偺偑恾3偱偁傞丅壒尮偑嬤偯偔偲偒偼懍搙偲嫟偵攇挿偑彫偲側傝丆墦偞偐傞偲偒偼懍搙偲嫟偵攇挿偑戝偲側傞偙偲偑傢偐傞丅
乮3乯丂僌儔僼偺夝愅
僌儔僼偼廲幉傪A偺揰偱愗傞捈慄偵側偭偨偺偱偁傞偑丆偙偺僌儔僼偺幃偼
兩=k亴-ku乧乧乧乧乧乧乮1乯
偲彂偗傞丅
k亴偼愗曅OA偱偁傝丆OA偼u亖0偺偲偒偺攇挿偱偁傝偲側傞丅
僌儔僼傪奜憓偟墶幉偲岎傢傞揰傪B偲偡傞偲丆B揰偼攇挿偑0偲側傞揰丆偡側傢偪壒懍偲壒尮偺懍搙偲偑堦抳偡傞揰偲峫偊偰傛偄丅偟偨偑偭偰
OB=v偲側傞丅k偼捈慄偺岡攝偱偁傞偐傜
偲側傞丅
偙偺k丆k亴傪乮1乯幃偵擖傟傞偲
偲側傞丅懄偪摦偄偰偄傞壒尮偐傜棃傞攇偺攇挿偼乮2乯幃偱帵偝傟傞偙偲偵側傞丅
偙偺攇傪惷巭偟偰偄傞娤應幰偑帹偵偡傞応崌偵偼
偺怳摦悢偺攇乮壒乯偲側傞傢偗偱偁傞丅
2丆娤應幰偺塣摦偵傛傞怳摦悢曄壔
乮1乯丂幚尡
嘆惷巭偺壒尮幵偐傜堦掕怳摦悢偺攇傪弌偟偰偍偒丆婰榐巻傪棳偟偰攇傪摓棃偝偣傞丅娤應幵傪摦偐偟丆婰榐巻忋偵娤應幵偺懪揰儁儞偺弌偡帪娫儅乕僋傪婰榐偝偣傞丅娤應幵偺懍搙u偼僗僩僢僾僆僢僠偱應傞丅
嘇懪揰儁儞偺怳摦悢傪應掕偟偰偍偒丆1昩娫偵壗懪揰偡傞偐傪偟傜傋偰偍偔丅
嘊婰榐巻傪尒偰丆娤應幵偑1昩娫偵婔偮偺攇傪僉儍僢僠偟偨偐傪挷傋傞丅
乮2乯丂寢壥偲偦偺僌儔僼
婰榐巻偵夋偐 傟偨僨乕僞乕偺堦晹傪恾4偵帵偟偨丅懪揰儁儞偺怳摦悢偼丆僗僩儘儃偱應偭偰丆1050夞/暘丆1昩娫偵17懪揰偱偁傞丅
乲恾亅4乴
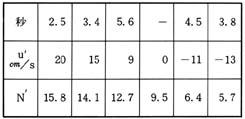
應掕寢壥傪師偺昞偵傑偲傔偨丅戞1棑偼娤應幵偑50噋恑傓帪娫丆戞2棑偼壒尮幵偺懍搙u亴丆戞3棑偼婰榐巻忋偺17懪揰娫乮1昩娫乯偵懳墳偡傞偢攇偺悢乮帹偵偡傞怳摦悢偵憡摉偡傞乯N亴偱偁傞丅
偙傟傪僌儔僼偵偟偨偺偑恾5偱偁傞丅娤應幵乮幰乯偑嬤偯偔偲偒偼丆懍搙偵嫟偵枅昩僉儍僢僠偡傞攇偺悢偑憹偟丆墦偞偐傞偲偒偼懍搙偲嫟偵尭彮偡傞偙偲偑傢偐傞丅
乲恾亅5乴
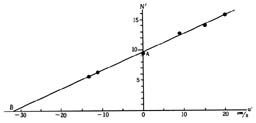
乮3乯丂僌儔僼偺夝愅
偙偺僌儔僼偐傜N=K亴+Ku亴乧乧乧乮1乯
偺幃傪嶌傞偙偲偑偱偒傞丅K亴偼N幉忋偺愗曅OA偱偁傝丆娤應幵乮幰乯惷巭偺偲偒帹偵偡傞怳摦悢偱乮v乧乧攇偺懍搙丆兩乧乧兩攇偺攇挿乯偲偍偔偙偲偑偱偒傞丅