|
段階時間
|
指 導 内 容
|
留 意 点
|
|
め
あ
て
を
つ
か
む
5分
|
1.天びんのつり合う様子を観察させ,本時のめあてをつかませる。
(1) てんびんのつり合いについて知らせる。
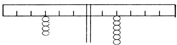
(2) めあてをつかませる。
|
○演示実験によって進める。

図の様に,うでの長さ(支点からの距離)に目がむくよう,テープをはっておく。
○めあては,板書する。
|
|
よ
そ
う
す
る
5分
|
2.どんな関係があるか予想させる。
(1) 比例しないことを確認させる。
(2) きまりがあることに気づかせる。 |
○演示実験から,うでの長さが長くなると,それに対応しておもりの重さが軽くなることに気づかせる。
※〔A〕に指名
(直感力にすぐれたものをもつので,この場面で活動させたい。) |
|
と
い
て
み
る
10分
|
3.うでの長さとおもりの重さの変化のきまりをみつける。
(1) 表を与える。

(2) 個々に,きまりをみつけさせる |
| |
| ○机間巡視により,次のような指導をする。 |
| |
・気づけない子-xが4cmのところをもとにして考えるとよいことをヒントとして与える。
・積一定,式,グラフなどに目を向けている子-xの変化とそれに対応するyの変化を先に調べるよう指示する。 |
|
|
た
し
か
め
る
15分
|
| 4.うでの長さとおもりの重さの関係を確認させ,反比例を定義させる。 |
| |
(1) 発表させる。 |
| |
|
| |
|
| |
|
| |
(2) 一方が2倍,3倍…になると,他方が1/2,1/3…になることを確認させる。 |
| |
|
○(4,300)をもとにして
○(8,150)をもとにして |
| |
(3) 反比例の定義を知らせる。
| 対応して変わる2つの量xとyがあって,xの値が2倍,3倍…になると, それに対応するyの値が1/2,1/3…になるとき,「yはxに反比例する。」といいます。
|
|
|
※〔B〕に指名
(もう一歩のがんばりが必要なので,机間巡視の際に指導の手を加えておき,この場面で発表させ自信をつけさせたい。)
○積が一定の発表に対しては,次時に学習することを知らせる。
○計算力に不安のある子にとっては,xが2倍になると,yは半分(1/2)は容易であっても,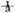 , ,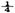 の理解は確認しておく必要がある。 の理解は確認しておく必要がある。
○一般的に,一方がm倍になっているとき,他方は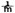 倍になることについては,第3時にあつかう。 倍になることについては,第3時にあつかう。
※〔A〕に指名
(まとめる力が,もう一歩なのでこの場面で言わせ,まとめることの大切さに気づかせたい。) |
|
ま
と
め
る
・
あ
て
は
め
る
10分
|
| 5.学習したことをまとめ,理解を強化する。 |
| |
(1) 反比例の定義をノートさせる。 |
| |
(2) 練習問題をさせる。 |
| |
|
①つぎの□の中にあてはまることばを書きなさい。
対応して変わる2つの量xとyがあって, xの値が2倍.3倍…になると,それに対応するyの値が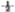 , ,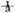 …になるとき「yはxに□する。」という。 …になるとき「yはxに□する。」という。 |
| |
|
②下の表で,yがxに反比例するのは,どれでしょうか。

|
| |
(3) 次事の予告をする。
|
| |
|
○表をたてに見たときのxとyの関係を調べる。 |
|
○机間巡視によって,解答状況をとらえ,個別指導をする。
○ の場合が反比例と判定されていないかどうかを特に注意して観察する。 の場合が反比例と判定されていないかどうかを特に注意して観察する。
※〔C〕に指名
(自信がもてず,周囲を気にする学なので,机間巡視の際にヒントを与え,はげます。)
|