研究紀要第63号 「教育課程の実施に関する研究」 -061/093page

　次に，この授業のまとめとして．課題の仮定から結論までの証明の流れを図示し，演繹的な思考力を高める助けとする。
　T　「それでは，この証明がどんな図形の基本性質を使って成り立っているのか，そのしくみを図に表してみましょう。

仮定AB＝CD		AB || 　CD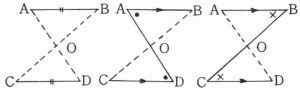
AB＝CD　　∠A＝∠D　　∠B＝∠C
		（平行線の性質）
	↓
三角形の合同条件を決定。
したがって 1辺と両端の角がそれぞれ等しいから 　　　　　　　△AOB≡△DOC 　　結論　　OA＝OD

　上のように証明のしくみを図示することにより合同条件を適用した推論の過程が明確になり，証明を簡単にわかりやすく表現するには，どのような順序で表現することがよいか明らかになる。その際，根拠として何を使ってよいか，またいけないか，図にあることのどれを使ってよいか，またいけないかなどについて指導し，それを通して，数学的な推論の意義が把握されるようにする。
　以上述べたように，第二段階において，証明の必要感を持たせる指導を通して，図形の証明に対する興味・関心を高めると共に学習意欲を育て，第三段階において，推論の筋道を正しく表現できる推論の能力を高めておけば，次の第四段階における証明の記述では，生徒が自信を持って学習に取り組み，証明を書くという表現能力が高まるものと考えられる。

6　おわりに
　図形の証明問題において，仮定から結論への正しい筋道を自分自身の力で発見し，それを適切な言葉や記号を用いて簡潔・明確に表現できたときの喜びや充実感は，生徒にとって格別のものであろうと思う。しかし，そのような数学的な推論の方法を理解して，論理的な思考力や表現力を育成することは，図形教育における最終的な目標とも考えられるので，一挙に達成できるほど容易ではない。
　そこで，中学校指導書数学編や他の文献等を参考にして，生徒の発達段階を考え，段階をふんだ指導計画などの工夫を通して論理的な思考力や表現力の育成のための研究を進めてきた。けれども，正しい作図の能力，用語や記号の的確な活用，そして，図形の基本的事項の理解などについての個人差が大きく，「主体的学習活動における個人差に応じた指導」「形成的評価を取り入れた授業で論理的な思考力や表現力の評価」など，いくつかの課題が残された。今後，残された課題の解決を図りながら，生徒が自ら考えて意欲的に証明しようとする魅力ある図形指導を創造し，論理的な思考力や表現力を高めるために一層の努力をして研究を深めていきたい。
　最後に，調査に協力していただいた先生方に対し，深く感謝するとともに，厚くお礼を申し上げたい。

〔参考文献〕
・中学校学習指導要領第2章第3節数学　文部省
・中学校指導書　数学編　　　　　　　　文部省
・教材研究のすすめ　　佐藤俊太郎　明治図書
・図形とその指導　　日本数学教育会編　明治図書
・図形と論理　　　　石谷　茂　　啓林館
・中学校数学科・3　新しい図形の指導事例　　大野清四郎・福森信夫編　明治図書
・最新中学校数学科指導法講座　1，4　　片桐重男：古藤怜・平岡患編　明治図書