研究紀要第63号 「教育課程の実施に関する研究」 -060/093page

たり，いろいろな観点から考察して証明をつくりあげる「証明の考え方」を指導しておくことが大切である。

仮定　←　○　←　△　←　口　←　結論 　仮定　→　○　→　△　←　口　←　結論 　仮定　←　○　←　△　→　口　→　結論 筋道を立てて整理してまとめる。 　仮定　→　○　→　△　→　口　→　結論

　このような「証明の考え方」は，単元を通して機会をとらえ，具体例を示しながら何回かくりかえし指導Lていくことが必要であろう。

課　題 右の図で，ABとCDが等しくABとCDが平行のとき　OA＝ODとなることを証明せよ。

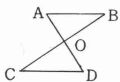
　課題を提示し，ノートに図を正確に作図させる。
仮定は青色，結論は赤色で図に印を記入させる。
　Pl　「まず，仮定はなんだっけ。」
　P2　「仮定は青で書いたからすぐ分かるよ。こことここが等しく，平行だよ。」
　Pl　「この図は．2つの三角形がきっと合同だよ。合同ならOAとODは等しくなるから。」
　P2　「そうだな。本当に合同かどうかわからないが，もし合同なら，結論が成り立つね。だから合同になることを言えばいいんだ。」
　Pl　「そうすると，ABとCDは等しい。この角は対頂角で等しい（∠AOB＝∠DOC）。」　AOとODも等しいぞ。」
　P2　「そこは赤色で結論だから使いないよ。」
　P2　「この角とこの角は同じだ。」
　Pl　「どうしてだい。」
　P2　「だって，こことここが平行だから錯角になっている角は等しいから。」
　Pl　「それじゃ，∠Bと∠Cも等しい。」
　P2　「そうすると合同条件のどれになるかな。」
　P2　「まず，3辺による合同はだめ。等しい辺はこことここだから……」
　Pl　「わかった。1辺と両端の角だよ。」
　P2　「よし，これで合同になることがはっきりしたから，OAとODが等しいことが証明されたぞ。じゃ，整理してまとめるよ。」
　ここで，話し言葉に近いものでよいから，ノートに簡単に証明をメモさせることもよいと思われる。（この時間に教師は机間巡視をして，つまずいているペアや個人に指導する。）
　T　「それでは発表してもらいます。じゃ，P2　君，前に出て来て発表してください。」
P2の発表例（図を見ながら）

「この2つの三角形が合同ならば，ここと．ここは等しくなります。2つの三角形は，1辺と両端の角がそれぞれ等しいので合同になります。それは，こことここが等しく，この角とこの角，あと，この角とこの角が等しいからです。だから、この三角形とこの三角形が合同なのでOAとODは等しいです。」

　P3　「∠Aと∠D，∠Bと∠Cが“平行線の錯角で等しい”と理由を言った方がいいと思います。」
　P4　「P2君の証明はよいと思いますが，こことこことか，この角とこの角のような言い方でなく，せっかく図に記号がついているのだからその記号を使って言った方がいいと思います。」
　生徒の発表をそのままの表現でOHPで見せてどう表現すればわかり易いか。また，P4のような指摘はなぜ大切なのかについて話し合わせる。
　口頭で述べさせる指導で留意することは，はじめは形式にとらわれない普通の話し言葉でよいから，図を指し示しながら推論の筋道を正しく言えるようにする。次に，図の記号などを用いて，「この三角形AOBとこの三角形DOCにおいて」のような数学らしい表現をさせながら，証明の形を整えていくように指導する。どの生徒も口頭で正しい推論がスムーズにできるようになるまで記述をさせないで十分に指導することが大切である。