福島県教育センター所報　第3号（S46/1971.10） -014/025page

(ｅｘ，１)　

　　　＿＿　＿　＿　＿＿　＿＿　　　＿　　　　　Ｚ＝ＡＢＣＤ＋ＡＢＣＤ＋ＡＢＣＤ＋ＡＢＣ　　　＿　　＿＿　　　　＿＿　＿　　　　　Ｄ＋ＡＢＣＤ＋ＡＢＣＤ＋ＡＢＣＤ

（１）２進数表示に変換する。

　　Ｚ＝Σ（００１０，０１００，００１１，０１１０，１００１，　　　　　１１００，０１１１）

（２）指数によって分類する。

（３）組合せを行なって変数を消去する。

　　　　２，３　　　００１−　　　　２，６　　　０−１０　　　　４，６　　　０１−０　　　　４，12　　　−１００　　　　３，７　　　０−１１　　　　６，７　　　０１１−

（４）　（３）で組合せを行なった項には（２）にチェック印を付ける。ただし，一つの項が２個以上組合せに使用されてもチェック印は１回だけ付ければよい。

（５）　（２）でチェック印を付けられた項を圧縮項という。
　　同様な方法で第二次圧縮項を作り出す。

(注)　ダッシュが同一列に並ぶこと，指数が１けただけ違うことが条件である。

（６）　この操作を組合せができなくなるまで繰り返す。

（７）　最後に残った圧縮項と，途中でチェックされなかった圧縮項を総称して主項という。この論理和が簡単化された論理式である。

　　　最後に残った項　　　２，３，６，７　０−１−　　　チェックされなか　　　　　　　　９　１００１　　　った項　　　　　　　　　　　４，６　０１−０　　　　　　　　　　　　　　　　　　　　　　　11，12　−１００

（８）　これらの論理和は，変数をつかって書くと

　　　　＿　　　＿＿　　＿　＿　　＿＿　　　　　　Ｚ＝ＡＣ＋ＡＢＣＤ＋ＡＢＤ＋ＢＣＤ

（９）　これらの論理和が完全標準形式（ＰＤＮＦ）の各項を重複して含んでいる場合があるので，ＰＤＮＦのすべての項を含む主項の最小組合せを結ぶため，次のような主項図を作る。

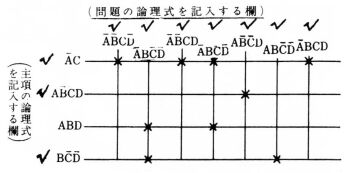（１０）　横列の項が，ある主項を含んでいるときは，その行および列の交点に×印をつける。

（１１）　一つの例と×印が１つしか含まないものに注目する。
　　　上図では第１列，第３列，第５列，第６列，第７列に×印が１つしかない。

（１２）

 　    　　　　　　　＿＿　＿　　　　　　　　＿　　　　　　第１列の項，ＡＢＣＤに対応する主項はＡＣなので，　　　　　　　　　　　　　　　　　　　　　　＿　　　　それにチェック印をつける。ついで主題ＡＣに含まれる　　　　　　　　　＿＿　　　＿　　＿　＿　　　　問題項を（ＡＢＣＤ，ＡＢＣＤ，ＡＢＣＤ）のすべてに　　　　　　チェック印をつける。

（１３）　次に，第３列の項を注目するが，すでにチェック印がついているので第５項に注目し（１２）の方法でチェック印をつける。

（１４）　次に，第６項に注目して同じようにくりかえす。そして問題項の各項に，すべてチェック印がつくまでこの操作をくりかえす。

（１５）　チェック印のついた主項の論理和が，最も簡単化された論理式である。

　　　　　　　　　＿　　　＿＿　　　＿＿　　　　（答）　Ｚ＝ＡＣ＋ＡＢＣＤ＋ＢＣＤ　 

Ｑ−Ｍ法による他の例題

（ｅｘ，２）次の主題図より論理式を求めよ。

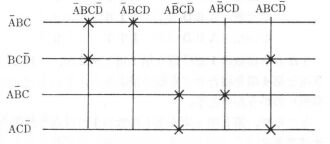このような場合はニつの異なった形ができる。