福島県教育センター所報ふくしま「窓」　No.132（H13/2001.2） -012/042page

シリーズ

学カ向上のための指導の在り方

～学力向上のための授業改善に関する調査・実践研究（中学校2年数学）から～

教育センター学習指導部

はじめに

教育センターでは、「学力向上」を目指した授業改善に資するため、平成6年度から調査・実践研究を行ってきた。

ここでは、一昨年、昨年と行ってきた実践研究から、「中学校2年数学」について述ぺる。

1　研究の視点

平成9午度に実施した学力到達度調査より、「1次関数」の中領域が低いことが分かった。本研究では、中学2年の「1次関数」を中心としながらも、他の学年の関数領域についても取り上げ、以下の4つの視点で実践した。

ア　図などとの関連によリ、1次関数について理解させる。

イ　対応表・グラフ・式の相互関連を図った指導をする。

ウ　関数指導にコンピュータを活用する。

エ　系統性を踏まえた指導をする。

2　実践研究

（1）「1次関数の指導」について（視点ア・イ）

教科書にある問題を次のように変え、提示した。

ぱねののびは、下げたおもりの重さに比例する。いま、10gのおもりを下げたときのぱねの長さが12cmであり、30gのおもりでは16㎝であるとする。

初めに、この事象を生徒一人一人が自分なりに把握し、それを図で表現する活動を取り入れた。その活動のあと、全体で確認する時間を設け不足した部分を付け加えた。ここでは、特に、「ぱねの長さ」と「ぱねののぴ」に注目させた。

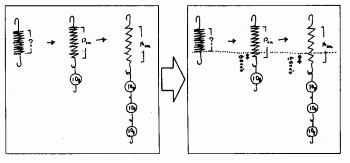
この図を見ながら、これらの長さとおもりの重さの関係について考えさせた。

「おもりの重さとそのときのぱねの長さ」の関係は、（ぱねの長さ）＝（もとのぱねの長さ）＋（おもりの重さに比例する長さ（ぱねののび））であることを発見させた。

これにより、xg　のおもりを下げたときのぱねの長さをy㎝　として、
y＝ax＋b　　（a,bは定数）
と表され、これを1次関数ということを理解させた。

次に、この1次関数をいろいろな方法で求めるという課題で展開した。1つの方法で求めたら、別の方法も考えてみるように促した後、それぞれの考えを発表させた。式、グラフ、対応表、図とを比例しながら、それぞれの求め方の違いや特徴について話し合わせた。

掲載情報の著作権は情報提供者及び福島県教育センターに帰属します。