§6演繹的な推論・証明

図形の証明における学習指導のポイント(中学校)

1　高等学校との指導のつながりを考えたときの指導上の配慮事項
(1)証明の必要性や重要性に対する意識を高めること
中学校の論証は図形分野に集中しており、他の数学の領域において、証明や論理的に推論していくことの必要性や重要性が認識されない傾向がある。
(2）題意を読み取って、条件を図として表現する力を伸ばすこと
条件を図に表して、題意を具体的にイメージ化させる指導が必要である。
(3)証明の過程で正しく仮定等を用いて推論を進める力を伸ばすこと
仮定と結論を混同し、推論の過程で結論を用いる誤りが多く見られるので、仮定から出発して、それまでに正しいと確認されたことがらを根拠にしながら、結論を導くということの理解に重点を置く指導が必要である。
(4)逆の考えを理解させながら指導すること
逆の考えを理解することは、論理的に考えを進める上で重要である。また、このことは、高等学校の数学Aの集合と論理とのつながりも深く、明確に指導しておく必要がある。


2　指導のポイント

【例】平行四辺形ABCDの対角線の交点をOとし、Oを通る直線がAD、BCと交わる点をそれぞれE、Fとすれば、OE=OFであることを証明せよ。
【考えの進め方】	【証明のポイント】
(1)題意を表す図をかきながら要点を把握させる。 (2）仮定と結論を取り出し、式で表すことができるようにさせる。 (3)結論がいえるためには、何がいえればよいかを考えさせる。 1）結論から仮定へと逆に条件をたどって考えさせる。 2）仮定と結論から連想できる既習事項の活用を考えさせる。 3）条件を適用できる図形を取り出したり、補助線を引くことを考えさせる。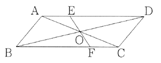	仮定:四角形ABCDは平行四辺形⇔AD//BC、AB//DC;AD=BC、AD//BC;AO=CO、BO=DO 結論:OE=OF 考えの流れ ↓ OE、OFを含む三角形を考える。 ↓↑ △AOE≡△COFが成り立てば OE=OFが成り立つ。 ↓↑ △AOE≡△COF示すには、 どの合同条件を使うか考える。 証明の流れ ↑