つなぎを含む確認問題(中学校)

1【基本の作図と関連する定理等を連想させることを確認する問題】
次の(1)、(2)を作図によって求めなさい。
また、(1)、(2)に関係する図形の性質や定理などで考えられるものをすべてあげてみなさい。(1)線分ABの垂直二等分線　(2)∠AOBの二等分線

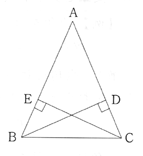
2【結論がいえるためには何がいえればよいかを確認する問題】 (1)右の図のように、二等辺三角形ABCの底辺BCの底辺BCの両端B、Cから辺AC、ABに垂線を引き、AC、ABとの交点をそれぞれD、Eとする。このとき、次の問いに答えなさい。 1）BD=CEを導くためにはどの三角形に着目すればよいか。 2）着目した三角形において何を示せばBD=CEがいえるか。 3）用いた条件を示してBD=CEを証明しなさい。
(2)平行四辺形において、対角線が内角の二等分線になっている。このとき、次の問いに答えなさい。 1）この四角形はどんな形であるか予想しなさい。 2）予想がいえるためには何がいえればよいかいいなさい。 3）予想したことを証明しなさい。
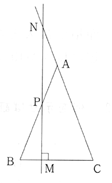
3【図をかいて考えることを確認する問題】 (1)AB=ACである二等辺三角形ABCの辺AB上に点Pをとり、Pを通る辺BCへの垂線が辺BC、直線CAと交わる点をそれぞれM、Nとする。このとき、△ANPは二等辺三角形になる。このことを証明しなさい。
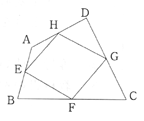
(2)四角形ABCDの辺AB、BC、CD、DAの中点をそれぞれE、F、G、Hとするとき、四角形EFGHは平行四辺形になる。 このことを証明しなさい。