○小学6年の比と中学2年の相似比に関する学習内容の比較

【小学6年の比】
●比の記号「:」の前の数を後の数で割った商を比の値という。
●a:bの比の値は,bを1とみたときaがいくつにあたるかを表している数。
●2つの比の値が等しいとき比は等しいといい,2:3＝4:6のように表す。

【何分の何倍という考えかたの例】
男子と女子の比が4:5で,女子の人数が20人であるとき,男子は何人か。
解)男子と女子の比が4:5なので,男子は女子の4/5倍だから,20×4/5＝16(人)

【中学2年の相似比】
●相似な図形の対応する部分の長さの比を相似比という。例えば,△ABCと△A'B'C'の相似比は2:1である。
●相似比として比の値を用いてもよい。相似比が2:1であるとき,相似比は2であるといってもよい。
●a:b＝m:nならばan＝bm(内項の積と外項の積は等しい)

(2)「a:b＝m:nならばan＝bm」の意味を,導く過程を含めてよく理解させる。
【内項の積と外項の積が等しい理由】
a：b＝m:nの両辺の比の値は等しいからa/b＝m/n　∴an＝bm
また,高校1年の三角比へのつながりを考えると,次の関係も押さえておきたい。
a:b＝m:n⇔a/b＝m/n⇔a:m＝b:n
このことは,正弦定理が,次のような比例式であることを理解する上で必要である。
a/sinA＝b/sinB＝c/sinC(＝2R)⇔a:b:c＝sinA:sinB:sinC　

(3)比の性質を用いる図形の相似の問題などを通して,比の有用さと比を用いる処理の仕方を身に付けさせる。
「どことどこが比べられるのか(比べればいいのか)」に着目させたい。
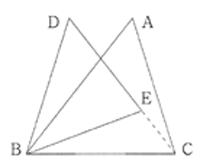
(例)右の図で△ABC∽△DBEであるとき,
ア　△EBCに相似な三角形はどれですか。
イ　アの2つの三角形の相似条件を答えなさい。
ウ　2つの三角形が相似であることを証明しなさい。