6　高校入試の文章題(図形)(中,高ともに)

図1のように,直線l上に1辺の長さが1mの正方形ABCDとPQ＝PR＝1mの直角二等辺三角形PQRがある。この△PQRを辺PQがl上にあるように右に移動させると,図2のように,辺QRと辺ADが交わるときがある。その交点をSとする。

AQ:QB＝2:3となるとき,△CQSの面積を求めなさい。
(H10高校入試6(1))(県正答率14.8％)
図1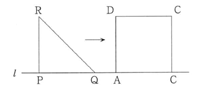
図2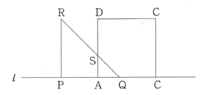

1　つまずきの内容と分析

(1)題意を読み取り,条件を図に表すことができない。
AQ:QB＝2:3を図2に書き込み,AQ＝2/5,QB＝3/5と求めることができない。

(2)△CQSの面積を求めるための解決の糸ロを見いだせない。
△CQSの面積をどうやって求めるのか,そのためには何がわかればよいのかがわからない。三角形の面積を求める方法が整理されて身に付いていない。

2　つまずきへの対策
(1)問題からわかる数値などを,すべて図に書き込む習慣をつけさせる。
○AQ:QB＝2:3を図に書き込む。
○△CQSに関してわかる数値を求めてみる。
AQ,QBの長さは比からわかる。QS,CQ,CSの長さは三平方の定理から求めることができる。
なお,CS＝CQに関して,図形の対称性などにも目を向けさせたい。

(2)結論を得るためには何がわかればよいのかを考える習慣をつけさせる。
○△CQSの面積を求めるためには何がわかればよいか?
→3辺の長さがわかれば求められるか?
(方針1)SQを底辺とみて,高さ三平方の定理で求める。
→他の方法はないか?(方針1が発見できないか,発見できても途中でつまずく)
(方針2)△AQS,△QBC,△DSCの面積を求めて,これらを正方形ABCDの面積から引く。(方法は小学校で学習)

(3)問題演習の際には,解答の方針を生徒に考えさせ,解法は分析的に示し理解させる。
○解答の方針とそのために必要な考え方や知識は何かを考える習慣をつけさせる。
○いかにして解答の発想を得たか,必要な知識は何か,を整理して生徒に理解させる。