5　高校入試の文章題(関数)(中,高ともに)

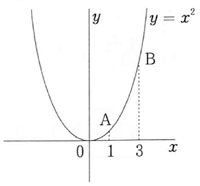
関数y＝x2のグラフ上に2点A,Bがあり,そのx座標は,それぞれ1,3である。このとき,点Bを通りx軸に平行な直線と,この放物線とのB以外の交点をC,直線ACとy軸との交点をPとする。
このとき,点Pを通り,△ABCの面積を2等分する直線の方程式を求めなさい。(H8高校入試5(2),県正答率13.3％)


1　つまずきの内容と分析
(1)問題文の意味がわからず,条件を図に表しながら題意を把握することができない。

(2）図から解決への糸口を見いだせない。
見当がついても,具体的に次のものを順次求めることができない。
○2点A,Bの座標→点Cの座標→直線ACの方程式→点Pの座標→△ABCの面積

(3)最終的にどうすれば答えが求められるのかわからない。
○△ABCの面積を2等分する直線とはどういうことか。
○何がわかれば,その直線の方程式を求めることができるのか。

2　つまずきへの対策
(1)問題文の意味を理解し,題意を把握するためには
○問題文を細かく区切って意味を考え,とにかく,図に表してみること。
「点Bを通り,x軸に平行な直線とこの放物線とのB以外の交点」とは何か?

(2)問題の条件を図の上で考え,それを式として表していくには
○条件から求めることができるものを連想すること。(考える材料を増やす)
○図示する際の作業の中で見つけられる条件に留意すること。
「点Cはx軸に関して点Bと対称だから,x座標は-」
○何をxとおくかも含め,文字を使って条件を等式として表すこと。
○2点を通る直線の方程式やy切片の求め方等の基本的事項の確認をすること。

（3）結論を得るために何をどうすればよいのかは
○条件を満たしたと仮定した図(こうなればよいという図)をかいて考えること。「△ABCの面積は,BCを底辺として考えれば底辺も高さもわかるので求めることができる。面積を2等分した三角形をPを頂点としてかいてみると,高さがわかるから底辺をいくらにすればよいかがわかる。その点とPを結べばよい。」