◆具体的な学習指導案3(平成11年11月船引中学校で実施)

	学習内容　・活動	一斉	一斉	○指導上の留意点　◆評価
課題把握	1　本時の学習課題が分かる( 1)既習事項の復習 <復習>次の問題の角の大きさや弧の長さを求めなさい。 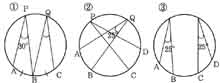AB=BCのとき、∠BQCは何度か。 AB=CDのとき、∠CPDは何度か。 ABの長さを3?とするとCDの長さは何cmか。 (2）課題を知る。 ■課題:1つの円で弧AB=BC=CDになるように、点A、B、C、Dをとる。さらにA　CとB　Dとの交点をEとすると、△B　C　Eは二等辺三角形になる。このことを作図して証明せよ。	一斉 個別 班別 一斉	7分	◆円周角と弧の関係が理解できたか。 ○机間指導をしながら個別に援助する。 ・下位の生徒中心 ○班で解答させるようにする。 ○班で発表させ、確認させる。 ○√A、B、Cの順に点をとらせるようにする。
課題解決の見通し	2　課題を解決する方法を考える ・作図する。 ・仮定と結論が分かる。 ・証明の手順が分かる。	個別 班別	8分	○机間指導をしながら、個別に援助する。 ・下位の生徒中心 ◆作図ができたか。 ◆仮定と結論が分かるか。 ◆証明の手順が分かるか。 ○班で確認させる。 ・図、証明の手順
課題追求	3　課題を解決する ・口頭で述べることができる。 ・記述する。 ・発表する。	個別 班別 一斉	2	○班での話し合いにより、証明の不得意な生徒にも、証明の流れが分かるようにする。 ・証明の流れをメモさせる。 ◆口頭で述べることができたか。 ◆記述できたか。
まとめ	4　問題演習する ■課題:1つの円で、平行な弦AB、CDにはさまれたAB、BDの長さは等しいことを証明しなさい。 5　次時の学習内容を知る。 ・直角と円周角	一斉	13	○ヒントが必要な生徒には、次の既習事項を確認させる。 ・補助線の引き方 ・平行線の錯角 ・円周角と弧の性質 ◆証明ができたか。できた順からプリントを提出させ、チェックする。 ○課題が終了していない生徒には、次時までの指示をする。