教育福島0011号(1976年(S51)06月)-017page

各領域のねらいや内容に照らして、内容相互の関連をとらえて、時には指導内容の再構成を図るなどによって、指導内容の重複をさけることもたいせつである。

もう一つは、児童生徒が学習しやすい、わかりやすい学習内容の配列に工夫することが必要である。毎時間の学習内容は、それぞれ新しいもので、児童生徒に創造されていかなければならないものであるが、この学習内容が全く新しいもの、むずかしいものという印象を与えては、学習に対して興味も意欲もわかないし主体的に学習を進めていくことはできない。また、これが学習時間のむだを起こさせている大きな原因の一つである。そのため、数学は系統性の強い教科であるという特性を生かして、既知と未知の学習内容の関連が、児童生徒にもよく理解され、学習に取り組めるような学習内容の精選と配列が重要である。

また、練習問題の学習は、学習能力の時間差が最も大きいものであることから、能力差を考えたり、フィードバックを考慮した出題が望まれる。

二、個々の内容のねらいや取り扱いの程度を明確に捕え、指導内容の統合を図り、教材を精選して指導効果をあげる。

(一)　単元の目標を明確におさえ、教材を精選すること。

指導内容の統合や教材を精選するとき、もっともだいせつなのは、単元目標を、算数・数学の目標や学年目標との関連で明確におさえると同時に、その取り扱いの程度を明確にすることである。

すなわち、例一に示してある単元目標、各時間のねらい、内容がそれである。このような形におさえることによって、学習内容の程度も明確になり、その学習において、どんな教材を配置したらよいか、取りあげられるべき教材が明確におさえられるのである。このことを、例一の第六時についてくわしく述べてみる。

第六時のねらいからは、次のようないくつかの教材が予想される。

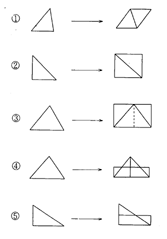
そのねらいと発展からの関係を考え合わせると、

○　1)は前時に台形を平行四辺形に帰着して考えているので、類推させると容易に理解できるので本時で取り扱う。

○　2)、3)は平行四辺形を見なおして、長方形で考えさせる柔軟な思考を育てる目的で次時で取り扱う。

○　4)、5)は取り扱わない。もし、児童が考えだしたときには、軽くふれる程度とする。

以上は、教材精選の一例にすぎないが、単元目標と各時間のねらいそれに児童生徒の思考様相などから考え合わせ、教材を再構成していくことによって、予想される教材のすべてをとりあげるのでなくて、学習のねらいにあった教材を精選して取りあげることができるのである。

(二)　生活経験の中から、数・量・図形の概念を抽象し、基礎的な理解や経験を得させること。

例一で取り扱っている台形、平行四辺形、三角形は、すべて抽象化され、もっとも単純化されたものである。それで、三角形を知っているということは、三角形の三辺や三つの角によって閉じた形という知識の理解以前に、いろいろな生活上に表れている「さんかく」の形をした平面が抽象されたものであるということを知っていなければならない。これなくして三角形を知っているとはいえないし、学習の結果が日常生活にも生かすことはできない。

数にしても同様であって、数は抽象化され、もっとも単純化されたものである。

例二は、日常生活の事象から3が抽象される過程を示したものだがこのようにして、3という数字は、を表す場合も、順序を表す場合もって、抽象化される過程で、その味が捨象されて数字だけとなる。から、3という数を一つあげてもの3という数が、その場に応じて本になったり、三着になったりすことがわからなくては、3というは知っていても、真の3という数の意味がわかったり、使ったりすることはできないのである。

〈例二〉　数字の抽象化の過程

以上から、抽象化された、もっとも単純化された図形や数字を使って学習する場面が多いために、よく理解させるためには、児童生徒の生活の問題にたちかえって基礎的な理