教育福島0015号(1976年(S51)10月)-039page

に良い分布が得られることが認められており、県標準テストは、この条件をほぼみたしている。

　

三、標準テストの活用

◎個人及び学級の位置づけと陥没点を知るために

(一)　領域ごと偏差値

研究主題設定の根拠として、領域の正答率をあげているレポートが多く見られるが、領域ごと偏差値を利用し、偏差値の五十と比較してみる。より厳密さを求めるならば平均の検定を行うことが必要である。次に検定のしかたを示す。

例　「ある学級三十六人の偏差値の平均が五十二である。」これは県平均よりすぐれているといえるか。

検定には次の式を用い、値が一・六五より大きいとき五。パーセントの危険率で有意差があると判定する。

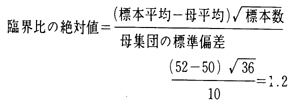
故に、県平均より良いと言えない。

(二)　小問正答率

小問の正答率は前述のように、ほぼ一〇パーセントから八○パーセントの範囲にある。これは導入としての取りつきやすさや、平均正答率を五〇パーセントに近づけるというような問題作成時の操作によるものなので、五〇パーセントからの上下によって判断することなく、つぎの到達率(一〇〇が中心)を判定の基準とすることが必要である。

(三) 全領域の偏差値

各領域の偏差値の平均をその教科の学力偏差値としているので、個人及び学級の教科の偏差値は、つぎの式を用いて算出する。

教科相互の成績を素点によって比較することは適当でないが、偏差値を用いることで比較が可能となるので、全領域偏差値によって教科相互の比較を行い、有意の差が見られるときは該当する教科の指導を重点的にすすめるというようなことが考えられる。

◎指導の反省と問題の吟味のために

(一)　尺度解析法(スケローグラム)による分析

スケローグラムというのは得点模様という意味で、正答誤答の状況を一覧表にまとめたものであって、問題の難易度と応答の傾向、個人の反応の安定度をは握しようとするものである。

スケローグラムを作成するには次表のように、問題を正答率の高いもの(易)から低いもの(難)へと順に並べかえまた児童生徒についても得点の高い順に並べかえる。

ついで、得点ごとに境界とみなされる線をひく、Aを例にすれば、Aの得点は六であるので左から六、右から四のところに線をひく、というようにしてその線をつなげば境界線が階段状にできる。問題の難易に対して、能力に基づく反応が理想的に現われるならば、境界線の左は全部1で右側は0となるはずであるが、現実には1と0が混入する。このことから児童生徒が能力に応じた反応をしたかどうかをみることができる。この混入度を数値として表そうとするのが次の式である。

混入率は0から一〇〇となるが数値の大きいほど、反応は不安定で信頼度が少ない。同様のことは問題の妥当性にも適用できるが省略する。

(二)　日新成就値

知能偏差値と学力偏差値の関係から児童生徒が能力相当に努力をしているかどうかを見るのに従来、つぎの式が用いられてきたが、これはテストの構成上、上にからく下に甘い値がでていたので、次のように修正された式を用いるのが良いといわれる。

以上研究過程において問題とされる初歩の検定の仕方について述べたが、スケローグラムについては小野寺明男著「教育研究法」▼佐藤隆博著「SP表の作成と解釈」にくわしい説明がある。

なお、活用にはなんといっても教師採点が前提である。

　

参考図書

○教育研究法序説　県教育研究所

○教育評価ハンドブック　梶原叡一

○教育と心理のための推計学

岩原信九郎

○教育評価の技術　橋本重治他編

　

スケローグラム

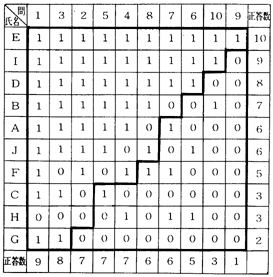
1は正答,0は誤答