教育福島0021号(1977年(S52)06月)-020page

1)中学校では、一意思対応として関数を抽象化しており、中学で学んだ例をとりあげて、写像の一般論を指導しておけば、関数は写像の特別な場合とするので、その後に指導する具体的な関数を統一的にみることができ、関数の合成、逆関数等は、写像の合成、逆写像等の一例として扱うことができる。

2)対応関係を強調するため、「関数とは一つの数式で表わされるもの」と、生徒が思いこむのを避けることができる。

3)関数の定義域、値域を印象的にうえつけることができる。

(2)(簡単な関数→写像)型

1)具体的ないくつかの関数を抽象化し、写像へと導くのであるから、写像をより具体的に理解させることになり、数学の概念構成のしくみを感じとらせるうえで効果的である。

2)生徒の発達段階と関数の発展の歴史的な経緯を考えるとき、この型の指導が、生徒の心理に、よりよく適合する。

3)「写像」を先に出すと、用語や記号による抵抗が先行して、いたずらに、生徒の理解を困難にする。

ここで少し私見を述べてみたい。

(簡単な関数→写像)型で指導するにしても、中学校において、既に関数を「一意対応」として抽象化しており、写像的見方もある程度身に着いていると思われるから、個々の具体的な関数の指導の場で、「写像」という用語は出さずとも、それを伏線として、指導することができるし、またそうすべきであろう。

また、写像の一般論については、深入りすることは、避けるべきであろう。高校では、基本的で具体的な関数についての指導が、重要だと考える。実質的な関数についてのじゅうぶんな理解があってこそ、写像概念もよく理解されるというものだろう。

　

表　(簡単な関数→写像)型

　

　

※(写像→簡単な関数)型は紙数の都合で略

　

四、高校数学における「写像」の位置づけ

歴史的にみた場合、数学の実質的な内容が、たいへん豊富になったとき、数学全般を集合と写像の概念で説明しようという考えが現れ、多くの数学的対象を、写像によって統一的に扱うようになった。

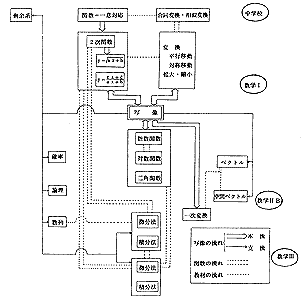
数学におけるこのような写像の役割りからして、高校数学での「写像」の扱い方も当然他の教材と異なることになる。他の領域との関連を考えながら写像指導の体系を組むにはどうすればよいかをみるため、次に、数学1)、数学2)B、数学3)の教材のなかで、写像の概念につながる系列を探ってみよう。

なお図において「写像の流れ→」では、必ずしも「写像」という用語を表面に出すということではない。

微分法、積分法で扱う関数は、写像としてとらえると、かえってわかりにくい面がある。ここで扱う関数は微分可能な関数か、連続関数であり、式で表されるものばかりである。その意味で特殊な関数であることを理解させ、動的な関数の考えに基づいて、ともに変化する量として関数をとらえるのがよかろう。

ここに至って、関数を写像として、とらえてきたのが、生かされないうらみもあるが、最大最小の問題では定義域、値域をしっかりつかまなければならないし、ここでの作用素は線形写像としてみられるし、合成関数の微分法では、関数を写像とみておくとつごうがよい。

　

五、おわりに

(写像→簡単な関数)型か、(簡単な関数→写像)型か、ということから筆を進めてきたが、いずれの型で関数教材を指導するにしても、高校数学のあらゆる領域のなかで、写像として見ることができるところでは、それに触れ写像の概念を深めていくことが重要で