教育福島0085号(1983年(S58)10月)-021page

数学

　

数学的に処理する応用例としての理科の教材

　

福島県立磐城女子高等学校

教諭　水野信

　

一　はじめに

　

高等学校学習指導要領に、数学の目標は、「数学における基本的な概念や原理・法則の理解を深め、体系的に組み立てていく数学の考え方を通して、事象を数学的に考察し処理する能力を高めるとともに、それを活用する能力を育てる」と示されている。ところで自分の授業を反省してみると、体系的な組み立てにウェイトが傾き、ときには抽象的・形式的な指導に流れる傾向もあった。そこで、少しでも生徒の数学に対する興味・関心を高め、数学を活用できるような態度を養うことを目標にして、他教科において数学的に処理される具体的な事例を見出し、これを教材化して数学の授業に取り入れるため、てはじめに理科について検討した。ここでは、その中から理科1)と数学1)との関連する分野について例を示す。

　

二　理科1)と数学1)との関係

　

(一)　指数計算と開平計算

数学1で指数を自然数から整数に拡張するが、例1、例2に見られるように指数計算には十分に習熟する必要がある。また中学校三年で筆算による開平計算を「研究」として履習しているが、これについても早期に復習を兼ねて確認し、理科1における計算に支障をきたさないようにする。

(二)　一時関数とグラフ

等速直線運動をグラフに表すと直線になるが、運動の特徴と直線の性質それに一次関数これら三つの相互の関係を見出すことによって、関数を身近な

　

(例2)指数計算　(例1)指数の拡張

　

(例3)等速直線運動のグラフ

　

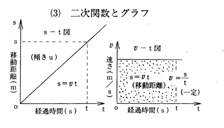
等加速度直線運動(例4)

　

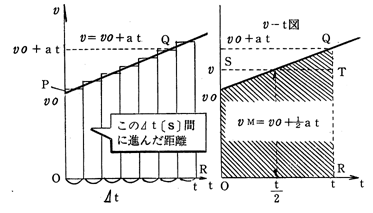
平均及び瞬間の速さ(例5)

　

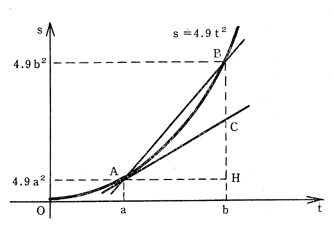
放物線の性質について