教育福島0085号(1983年(S58)10月)-022page

ものに感じるようにする。(例3)

(三)　二次関数とグラフ

関数の「変化の割合」は、中学校三年で履習する。その例を「斜面で転がるボールの時間と距離」(等加速度直線運動)にとっていて、「変化の割合」を「平均の速さ」に結びつけているので、数学1)においても同様の扱いをして、更に直感的にとらえることによって「平均変化率」の極限まで発展させて「瞬間の速さ」に結びつける。

また、放物線上の一般の点における接点の方程式を求めて「接点の傾き」と「瞬間の速さ」を結びつける。なお物体の運動とグラフと二次関数の相互の関係については、一次関数の場合と同様に扱う。(例4・5)

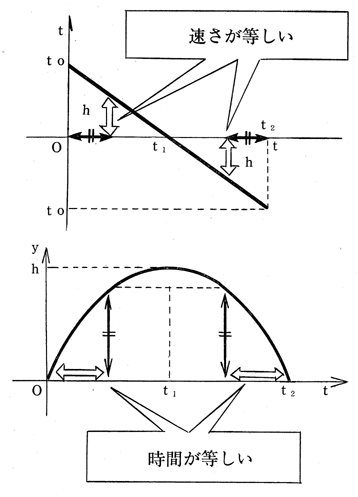
放物線の性質について、鉛直投げ上げ運動を例にとると、次のような説明ができる。(例5)

1　ある高さまでに達する時間と、その高さからもとの位置にもどるまでの時間が等しい。

2　同じ高さでの速度は大きさが等しく向きが反対である。

(四)　三角比(例6)

　

三　おわりに

　

これまで、数学の授業にこのような教材を取り入れてきたが、生徒は高い関心と興味を示し好評であった。今後は他の教科についても授業に計画的に折り込んでいこうと考えている。

なお、選択科目の理科と数学の関係については、その内容を対比させる形で右の資料にまとめてみた。

　

参考資料

教科書理科1(数研出版)、教科書物理(大原出版)

教科書化学(大日本図書)、教科書生物(実数出版)

教科書地学(東京書籍)、新理科1)図版(数研出版)

　

(4)　三角比　(略)　(例6)

　

資料　数学と理科1)との関係

数学と物理・化学・生物・地学との関係は略

　

美術

　

美術通信からカルトンの制作まで

　

福島県立富岡高等学校

教諭　谷田部健二

　

本校では、入学時に、音楽と美術のいずれかを生徒に選択させているが、美術の選択者の動機は、なんとなく美術を学習してみようとする者、絵画に