教育福島0109号(1986年(S61)02月)-041page

ればよいかという見通しがもてたときである。自己学習能力を構成する一つの側面として、学習目標を見つけていく力を育てなければならないわけがここにある。

1)　一単元でのプランの立てさせかた

児童に対して、次のような学習計画の立てかたを指導する。

ア、新しい単元名の意味を考える。また、学習する内容を概観してみる。

イ、今まで学習したことで不十分なところを、準備テストや教科書をもとに復習しておく。

ウ、事前テストや教科書をもとにして、これから学習することを見通す。

エ、学習する順序を知り、学習課題(又は学習すること)を見つける。

オ、単元で必要な、学習用具を準備しておく。

以上のようなことについて、単元の学習に入る前に一時間を組み、オリエンテーションを行う。

−学習計画立案の実践から−

まず、　「小数のかけ算」での実践であるが、何の手だても加えなければ、自ら課題を見つけ出すことは、かなり困難な状態であることがわかる。上位の児童でも空欄が多く、また、記入されていてもポイントのずれたものが目立つ。

しかし、次の「小数のわり算」の単元になると、かなりの部分まで課題を見つけている。ここでは、小数のかけ算で学習した学び方を、大いに参考にさせたからである。これら二つの単元は、学習の流れに共通部分が多いことに気づかせ、小数のかけ算との違いは、等分除と包含除の違いがあること、乗法との逆算関係や余りのある除法などであることをしっかりとおさえた。

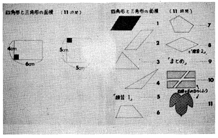
「四角形と三角形の面積」では、TPを用いて行った。(資料2)

以下はその指導の概略である。

「これは四年生で学習した形だが、面積を求められるね」

−正方形と長方形を提示

「では、これらの形はどうだろうか」

−マスキング法により、徐々に未習の形(平行四辺形等)を提示する。

「四年生で学習した形と違う点は何だろうか」

−全て基本単位となる正方形を敷きつめることができない図形であることを、一平方センチメートルの正方形を動かしながら、明らかにした。

「どうしたら面積を求めることができるだろう」−長方形や正方形では、単位面積のいくつ分という考えから、たて×横という公式を考え、たてと横の長さに目を向けた。「平行四辺形、三角形、台形などではどうすればよいか」と問題をなげかけだ。

「学習する順番を決めよう」

−事前テストによると、面積が求められた図形は、平行.二辺形の四名だけであり、他の図形の正解は皆無であった。

「まず、四名の人ができていた平行四辺形から始めることにしよう」

「学習する順序は,このようになります」

−番号を書いてあるTPシートをオーバーレイして提示し、学習の順序を明らかにした。

「台形の学習がすんだあと、どんな形の面積を求める学習をしようか」

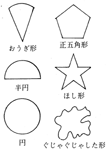
−事前テストに自由に書いたものの結果を発表させると、次のような形の面積を求めてみたいという人が多かった。

−正五角形とほし形については、第7時：多角形の面積の中で、ぐじゃぐじゃした形については、第11時：面積の求めかたの工夫の中で、おうぎ形、半円、円などについては、単元10「円と正多角形」の中で、というように指導計画に位置づけた。

学習課題を見つける作業は、学習の遅れがちな児童にあっては、なかなか困難な作業ではある。しかし、前述のような手だてを講じた結果、かなりのところまでできるようになってきた。

2)　一単位時間における解決の計画の立てさせかた

一単位時間において計画を立てる場は、指導過程五段階の中の、　「課題をつかむ」「見通す」段階である。

ア、課題をつかむ

ここでの課題把握には、あまり時間をかけなくて済む。単元全体を通しての課題づくりが既に行われているからである。児童からの発表をもとに、それらの異同を話し合い、一つの課題としてまとめさせた。

イ、見通す

　

資料2　学習計画で用いたTP