教育福島0135号(1988年(S63)11月)-018page

る総合化の二つの視点」、社会科教育研究No.57,1987。

　

数学

三角比(関数)での測量実習の試み

県立湖南高等学校

教論　熊谷　昭二

　

一、指導計画への位置づけと目的

　

数学1)から数学2)への内容が徐々に概念中心となり、実際、身の周りに数学が潜んでいることを実感できずにいる生徒が多数である。そして、教える側もまた、ただ単に問題の解法のみの指導に陥りがちである。様々な能力を持った生徒に活動の場を与えるとなると、困難を感ぜずにはいられない。

一つの試みとして三角比(関数)の導入または応用として、簡単な測量実習(トラバース測量)を実施した。単純な方法で面積を求めることができ、教室での学習内容が活用されていることがわかると考えたからである。

以下、測量作業の方法、手順等を示すが、専門用語を〔　〕で示すことにする。

　

二、測量方法とデータ計算の手順

　

作業1　野外での測量データ採取

平地に測定地点〔測点〕を任意に取らせ、巨大な多角形〔閉トラバース〕を作らせる。この形は何角形でもよく、また、測点と測点の間に障害物がある場合は補助点を取らせる。一余弦定理の活用)

次に、巻尺と分度器で辺の長さ〔測線：mi〕と測点上の内角〔交角：ai〕を測定させ、簡単に記録させる。さらに、一つの測点で北方向から次の測点までの測線への角度〔仮北からの方向角：b〕も記録させる。(図1参照)

メモには、測線の長さの単位を1/100角度の単位を度までとして記録させる。トランシットを用いれば、交角を秒単位まで測定できるが、細かな角度は計算処理上困難をきたすので避ける。

この作業は学校の駐車場で行ったが、生徒たちは真剣に活動し、データを採取した。

　

作業2　交角の調整

幾何学的にn角形の内角の和〔幾何学的条件：180°×(n-2)〕と、内角の和〔交角の和：Σai〕を比較させ、誤差〔角の閉合誤差：E=Σai180°×(n-2)〕がどの程度あるか計算させる。この誤差を各交角に分散し、交角の調整〔調整交角：ak=ai-n/E〕を行わせ幾何学的条件を満足させるようにさせる。(表1では誤差が5°あり測点数が十か所のため、式のとおりでは交角が分単位になってしまうので、任意の測点五か所だけに分散させた。)

　

作業3　交角を方位の角に変換

作業1で測定しておいた仮北からの方向角βと交角akを基に、順次測点での南北軸とのなす角〔方位の角：θk〕を幾何学的に求めさせる。

全生徒で行うことは困難なため、前もって生徒三名で算出させたが、かなりの時間を要した。

　

図1)　測点と測線

　

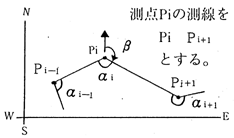
図2)　台形の面積

　

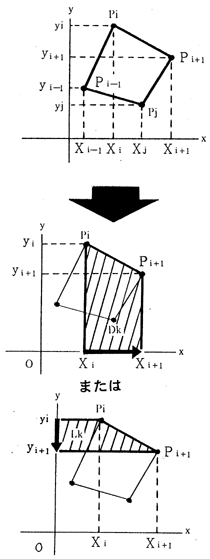
作業4　三角比(関数)表の利用

作業3で得た方位の角の正弦と余弦の値を電卓や表から求めさせ、さらに＋や−の符号を付けさせる。(表1cosθk,sinθkの欄参照)その後に測線との積を求めさせ、南北方向と東西方向の各成分に分ける。〔南北方向成分を緯距：Li＝mi×cosθK、東西方向成分を経距:Di＝mi×SINθk〕

また、緯距と経距のそれぞれの和を求めさせる。〔緯距の和、緯距の閉合誤差：ΣLi、経距の和、経距の閉合誤差：ΣDi〕

これらの作業は、生徒たちにとって容易であったため、作業は速かった。作業5　測線(緯距、経距)の調整

緯距、経距の閉合誤差を各測線長ヘコンパス法則により比例配分させる。

〔調整緯距：Lk＝Li−(ΣLi×mi/Σmi)、