教育福島0135号(1988年(S63)11月)-019page

調整経距：Dk＝Di−(ΣDi×mi/Σmi)〕

この作業も放課後三名の生徒に行わせたが短時間で終わった。また、測線の調整は、

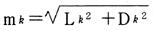
でできるが、あえてせずに終えた。

　

作業6　座標への変換

適当な測点を選び、南北方向と東西方向の座標に変換させる。(表1)参照)南北方向をy軸に、東西方向をx軸に取るため、測点P6のy座標を0に、測点P9のx座標を0とし、逐次左回りに調整緯距、調整経距を加算していけば、各測点Piのy座標、x座標が求められる。〔Y6＝0,Yk＋1＝Xk＋Lk,X9＝0,Xk＋1＝Xk＋Dk「Kはトラバースを一周するようにとる」〕

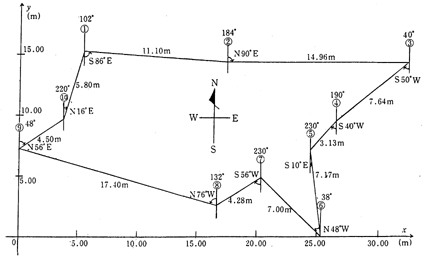
なお、図3)はこの座標を基に生徒が測点を記入したものに、数値を付記したものである。測点、測線の全容〔トラバース〕がはっきりと示されている。

　

作業7　マクロの区分求積

図2)のように、トラバースを台形に分割し、その面積の和によって全面積を求めさせる。台形の上底と下底の和〔倍縦距：Yk＋Yk＋1,倍横距：Xk＋Xk＋1〕を求め、高さ〔調整緯距：Lk,調整経距：Dk〕を掛けさせ、〔倍面積：Dk(Yk＋Yk＋1),Lk(Xk＋Xk＋1)〕それぞれ総和を求めさせる。

前者を男子に、後者を女子に分担した。男子の倍面積は正の値、女子のは負の値となるが、それらの絶対値は同じ値になる。

最後に二等分すれば、トラバースの面積が求められる。

この作業7で生徒たちは、男女ともグループに分かれ、一つ一つ確認し合いながら楽しく計算に取り組んでいた。

(表1は男子の計算結果である。)

三、測量実習とその成果

授業時間では三時間。放課後まで取り組んだ生徒はさらに三時間を費し、終了した。巻尺と分度器というありふれた教具だけで、角の閉合誤差5、測線の閉合誤差1.03mの結果を得た。測量の誤差許容制限2/100％には程遠いものではあるにせよ、学習内容を駆使して簡単なメモから面積を求める基本的な作業を成し得たことは確かである。

作業をとおして生徒から「本当に面積を求められるの？」とか、「本当にこれが面積なの？」とかいう声があった。驚きや疑いを持ちながらも、本校生の場合、作業を好む者が多い。教室内の授業では静かであるが、野外での活動では活発に、表情も生き生きとして、成果も多かったと確信している。

今後も作業などを取り入れた学習を展開していきたいと考えるが、生徒と教師側の活動内容・準備・手順を明確に示しておくことで、一層生徒が自主的に活動できるよう留意し指導にあたっていきたい。

　

表1)　測量データ(S56.6.18採取)と計算作業結果(subscript　iは調整前を、Subscript　kは調整後を表す。)

　

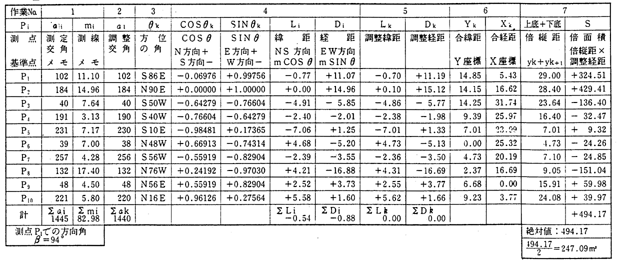
図3)　トラバースの全容