小学校福島県診断標準学力検査問題分析結果報告-014/63page

[4]量と測定

[4]量と測定

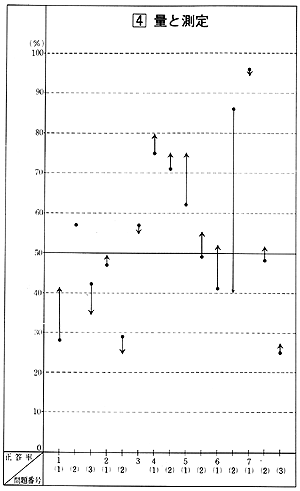
　この領域全体の伸びが,46年度と比較して3.0%の差だけであることからも分るように,小問ごとの正答率も,上のグラフに示されているように,大きく落ちこんだものがあったりして、指導の成果が表れていない嫌いがある。
　領域全体の正答率が54.0%と,5つの領域の中では最も低い数値を示している。この領域全般にわたって,指導法の工夫と改善が必要と思われる。
　この領域での指導のねらいの一つとして,メートル法の特徴やそのよさを理解させることがあるが,いわゆる単位換算の問題は,ほとんどが50%を割る低い正答率になっている。(1(1)〜(3),2(1)〜(2))
　とくに,1(2)〜(3),2(2)は,46年度における正答率より低い正答率を示していることは,メートル法の指導のあり方に基本的な改善が要求されていると考えてよかろう。
　メートル法では,数量の取扱いを能率的に活用させるために,日常生活で経験できるものと関連させた取扱いが大切であると同時に,メートル法の単位のしくみの特徴としてあげられる次の二つの性格が不十分であると考えられる。
　　 ●補助単位が十進法のしくみによって決められていること。
　　 ●基本的な量をもとにして他の量の単位が誘導されるしくみになっていること。
　したがって,今後の指導においては,単位換算が単なる記憶をもとにした換算の練習にとどめることなく,ディメンジョンを考えた問題として,単位の十進構造とともに,より効果的な指導法の改善が必要となってこよう。
　したがって,今後の指導においては,単位換算が単なる記憶をもとにした換算の練習にとどめることなく,ディメンジョンを考えた問題として,単位の十進構造とともに,より効果的な指導法の改善が必要となってこよう。
　次に,立体図形の表面積を求める問題として6(2),7(3)があるが,ともに低い正答率を示している。とくに6(2)は,46年度と比較して,45.5%もの正答率が低くなってきていることは,表面積ということばの正しい使い方を理解していない結果と考えられる。同じ表面積でも,7(3)がより低い正答率を示しているのは,前者は直線図形であるのに対して,後者が円であるために抵抗があったためと考えられる。