小学校福島県診断標準学力検査問題分析結果報告-015/63page

[5]数量関係

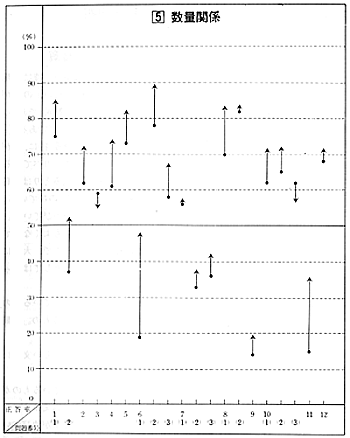
[5]数量関係

　全体の平均正答率が62.6%で,46年度と比較して正答率で8.3%の伸びであるが,上のグラフからも分るように,小問ごとの正答率に大きなバラツキがみられる。
　正答率が50%を割っている小問も5題あり,46年度に比して正答率が低くなったものも2題ある。
　この領域では,関数的な面と統計的な面の2つに大別される。関数的な考え方については,これまでに各学年で積重ねてきた目標を,ここで比例などの関数関係の理解,活用という点で総合し,比例や式,グラフなどを通して目標を完結するようになっている。
　また,統計的な数量関係では,可能性の集合作りなどを通して,分類,整理などの考え方を発展させて確率の素地指導をすることになっている。
　この領域で最も低い正答率を示したのは9で,問題は「貯金の 20% にあたる 480円 をおろした。おろすまえの貯金高を x円 として式を立てよ。」である。正答率が20.3%であることからも分るように, x , 20% , 480円 の3者の量関係がつかめなかったのが大部分である。また,“〜にあたる〜”という“あたる”ということばのとらえ方に大きな低抗を示していたものがみられるし,さらには,20%の意味を式表示するのにとまどいをみせていた児童も多い。誤答例として, x×20＝480 の式が多いことからみても分る。今後の指導に改善が必要であろう。
　7(1)〜(3)は,いろいろな量関係の中から,比例するもの,反比例するもの,比例も反比例もしないものと分類してえらび出す問題であるが,予想どおりの低い正答率を示している。第6学年での関数指導は,中学校での比例の一般的な式表現,さらには,一般の比例関係に発展させるための素地指導として重要な意味をもっている。比例や反比例関係を,ことばや表やグラフから判別したり,3者の関係を自由に往復できる指導を十分にしておくことが大切になってくる。
　11は,統計的確率とよばれるものを,実験データから推測する問題であるが,確率指導における実験の位置ずけや蓋然性を表す数値の意味など,もう一度基本にもどった指導の工夫が必要である。