研究紀要第6号 学習指導改善に関する研究 理科実験 - 034/036page

図5　pH3．3で反応させたときの変化

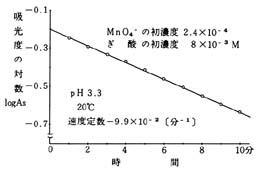
図5から，一次反応とみなして，速度定数を求めると，9．7×10^-2〔分^-1〕の値を得る。

5．考察

（1）　教材としての取り扱い。

A→生成物　という反応で，反応の速さがAの濃度に比例する場合，Aの初濃度をa，時間ｔにおけるAの濃度を（a-x）とすると，



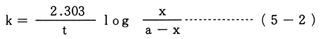
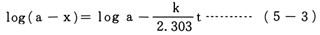
このような数式変形を理解できる場合は，図3，図5のようなグラフを書いて，結果を考察させることもできるが，高校では，数学との関連もあり，取り扱いにくい。
高校段階では，次のような扱い方が適当と考える。
�@吸光度の変化のグラフ（図2）を見て，の消失速度がだんだん遅くなることに，まず，気づかせる。
�A各時刻における平均の速さ（吸光度の平均変化率）を計算させる。例えば，1．5分後の平均の速さ（As/分）を，1分後と2分後の吸光度の差から求める。
�B各時刻の平均の速さとの濃度（吸光度）の関係をグラフに書き，考察させる。
�Cグラフ（図6）から，一定の時間までは，反応の速さが，の濃度に比例していることを確かめる。
�D反応の終わりの方では，マンガン酸化物のため，比色定量が妨げられていることを，観察事実（溶液の色，長時間放置したときの沈でん生成など〉から，指導する。

図6　各時刻における平均の速さの濃度

�E　数式を用いる場合は，次の程度とする。
反応の速さが，の濃度Cに比例するとすれば，dc/ｄt=kc　したがって，
dc/dt÷C=k（一定）
（平均の速さ）÷（濃度）≒一定
この関係が，成り立つかどうかを，表3のようにして確かめる。

表3　データ処理の例

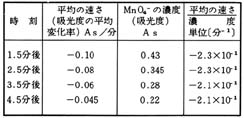
（pH6．9，の初濃度2．4×10^-4M）

（2）　測定条件について

（1）で述べたように，高校では，測定した吸光度の値をそのままプロットしたグラフ（図2，図4）を用いる方が，指導しやすい。しかし，図4のグラフ（pH3．3で反応）では，変化が小さく，反応の進行にともなう速さの変化がはっきりしない。pH7の条件で反応させた図2のグラフならば，速さの変化がよくわかる。この測定では，反応の速さを適当な速さに設定することが必要である。pH7のときの反応の速さ（速度定数−2×10^-1〔分^-1〕）ぐらいが適当と思われる。
なお，pHの値によって反応の速さが変わるの