研究紀要第16号　学習指導改善に関する研究 理科実験 - 009/020page

データの考察から，次のようなことが考えられる。

〔表4〕

（1）　a×b	720	450	400	408	559	720
（2）　a＋b	72	45	40	41	56	72
（1）÷（4）　f	10	10	10	≒10	≒10	10

　すなわち，a×bの数値とa+bの数値とが同じになるか。または，近似値になるから，この考えは正しく，次の式が導かれる。
（a×b）÷（a+b）＝10＝f（焦点距離）この式の値は，あらかじめ測定しておいたとつレンズの焦点距離と合致する。しかし，このような方法ばかりで，うまいデータが得られるとは限らない。したがって，どうしてもグラフ化の指導が必要である。また，常識を越えた変則的な手法によるが（a，b）という座標をプロットするのではなく，X軸上のaと，Y軸上のbとを，直接，直線で結んでしまう。このような直線は，1点で交わり，その点の座標はX，Yともに，実験に用いたレンズの焦点距離に等しい。

　したがって，焦点距離のわかったレンズを用いるほうが，生徒の思考を育てるのに有効である。このようなグラフ化の指導は，生徒の自由な発想を決して制限するのではなく，むしろ発見の喜ぴを体得させるものである。
　このグラフによれば，発見した規則性を使って，別のaに対応するbを予想することができるし，未知の焦点距離さえも求めることができる。

　さらに，実験して，それらを確かめれば，規則性の正しさが証明される。
また，なることから，この式を変形すると，ab＝f（a＋b）となり，ab＝af＋bfとなる。この式の両辺をabfで割ると，または，f^-1＝b^-1＋a^-1となる。
　このように，公式を教える必要はなく，このグラフが公式の役割りをじゅうぶん果たしているのである。
　このグラフを活用する生徒は，a＞fの場合のbを予想するだけでなく，a＝fやa＞fの場合にまでおよぶであろう。

　その結果，（図5）のようにして，b＝∞やこれまでとは違う像の位置（a＞fの場合とは反対側に像ができるのではないかと思う）を発見する。それが，平行光線や虚像に発展していくのである。

（図5）

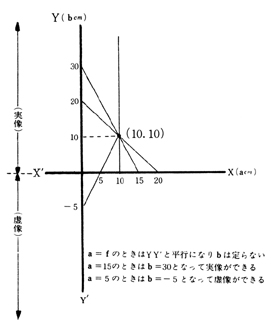
　このようにデータの処理の指導を適切に行なえば，公式にかわるものとして，グラフが大きな規則性を示すことを発見することができる。そして，像のできる位置や像の大きさを，幾何光学的に解明することになり，実像や虚像のできるわけが説明される。

4．おわりに

　この学習の実験方法は新しいものではなく，各学校にある実験装置を用いて正しい測定をおこない。そのデータ処理と考察に重点をおき，グラフ化の指導を強調した1例を示しているので，まだまだ，種々の開拓と問題点を残しているので今後も研究をすすめていきたい。

　参 考 文 献

○中学校理科指導書（文部省）
○大日本図書指導書
○東京都研研究報告書（中学校理科学習評価の現代化）
○中央現代化講座テキスト