研究紀要第24号 中学校 福島県診断標準学力検査問題分析結果報告書 - 059/106page

れる。
　したがって，指導するときは，集合の表記とその図示のし方を明確におさえる必要がある。

【4】　図形
問題2
　ねらいは，円すいの展開図から円すいの高さを直角三角形の性質を用いて求めることや一辺の長さと一つの角の大きさ（60度）が与えられたとき他の辺の長さを求めることである。
　この誤答は，（1）では

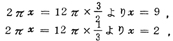
意味不明の解答であり，（2）では（1）の誤答が原因で誤ったものが目立ち，（3）では一つの角の大きさが60度である直角三角形の性質の不正確な知識・理解にょる誤りが目立っている。
　したがって，学習結果がどの程度定着しえるか学習の出発点として何をおさえるかなどに留意して指導することが必要であると考えられる。

問題4
　これは，三平方の定理を空間図形にも活用できるかどうかをねらったもので，数学的考え方の程度を総合的にみようとする問題である。，
　これの誤答の傾向は，�p，3a�p，3a²�pなど意味のある誤答よりも，a�p，a²�p，1．5�p，a�p などの意味不明の誤答が多いことである。
これは，空間図形の性質を考える場合に，平面で空間図形を切って，その切口の図形を考えるのが合理的であることなどの基本的な考え方が身についていないことを意味するものであろう。
　したがって，基本的な考え方の指導には時間をかけ，それの定着化をはかることがたいせつであるといえる。

問題5
　これは，二つの球の位置関係についての知識・理解の程度をみることをねらいとしているが，その誤答の大部分は5＜d＜8である。
　したがって，知識・理解の不足よりは指導のまずさとみることができる。
　i．e．基本的な知識とそうでない知識とを指導者は正確におさえて効果的に指導しなければならない。

問題6の（2）
ねらいは，円周角と弧の関係についての知識・理解の程度をみることであるが，誤答はAC，ABC，AC，であるので，その原因は表現の不正確さにある。
　したがって，問題の意味から判断して，どの程度に表現するのがよいかを決めて解答しなければならないことも指導する必要がある。

問題8
　これは，円に内接する四角形の性質を用いて推論するもので，そのねらいは数学的考え方の程度をみることである。その誤答の多くは，点P，点Qであるから，問題に与えられた図形から視覚的に解答を求めたものといえる。
　したがって，推論の難しい問題に対して生徒は安易にとりくむと考えられる。これは，学習指導における学習態度のしつけの問題である。

問題10
　ねらいは，数学的考え方の中の論証の能力の程度をみることであるが，その誤答の原因は，問題から仮定と結論を読みとれないこと，推論の仕方が理解されていないこと，表現能力の低さによると考えられる。
　したがって，この指導においては段階にしたがって一歩一歩理解させるようにすることも重要であるが，生徒の直観から論証の筋道をうみださせることがよりたいせつであろう。

　

むすび

既成の検査問題の検討，学習指導要領と教科書の分析をとおして，妥当性・診断性・信頼性についての論理的考察をし，また，予備テストの結果を尺度分析法により実証的に考察した。

　この考察の結果をまとめたものが，前述の問題作成の基本方針である。
問題構造が学習指導要領の指導内容に対応づけてあるという意味で，系統的・段階的，発展的に問題が構成されていることを明確にするために，問題のねらいを示した。
　また，生徒の学習結果を診断するときに，学習上の問題点を全県的位置づけでとらえられるようにするためと，診断の参考例を示すために正答率をあげ結果の考察をした。

したがって，テスト結果の科学的考察が可能となるので，学習指導改善の資料として十分に役立つものと考える。