研究紀要第38号 学習指導に関する研究 - 025/081page

ところで，この（ ）内の交項級数は，条件Aをみたしているであろうか。もし，みたしていれば，項打ち切りによる誤差の評価がなされる。
（ ）内の交項級数の第n項と第（n＋1）項とをそれぞれUn，Un＋1とすれば，

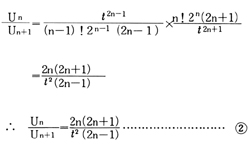
ここで，tは高々4ぐらいまでの値であるから，nをある程度大にすれば，�Aの右辺を1より大にすることができる。実際，

t＝1，2のときは　n≧1で t＝3のときは　n≧4で t＝4のときは　n≧7で

}

……�B

�Aの右辺は1より大になり，条件Aをみたすことがわかる。したがって，これらの項以上までの和を取れば，項打ち切り誤差の評価ができるから，あらかじめ項打ち切り誤差の大きさεを決めておけば，その大きさが，εより小になる項（かりにUn＋1とする）の一つ手前の項（Un）まで，この級数を計算すればよいことになる。
　なお，計算に際しては，次の漸化式

を用いて，次々に項を求めるプログラムをつくり，項打ち切り誤差が，εより小になる項（Un＋1）の一手前の項（Un）までこの級数を計算するようにした。

（表9−1）は，t＝1（S）から，1（S）きざみで4（S）まで，おのおのの場合の項打ち切り誤差が10 ⁻¹⁰（S）より小になるまで各項を計算して，最終的にその和（確率）p（t）を求めたものである。
�@の□内の三段重ねの数字のB◇は，t＝1