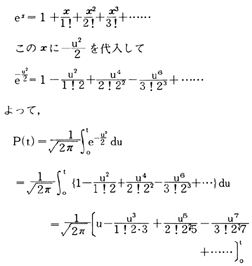研究紀要第38号 学習指導に関する研究 - 024/081page

は“きざみ”である。{　｝中の交項級数は，あらかじめ定めたεよりも，項打ち切り誤差が小さくなるまで計算させるようにする。
　微積分の本には，技巧をこらした展開式

があげられているが，電卓で計算させる場合，上記の方法で十分精度の良い値が得られる。

7．二項分布表

　二項分布表は，Pγ，Pγ−1に関する次の漸化式を用いて作成する。

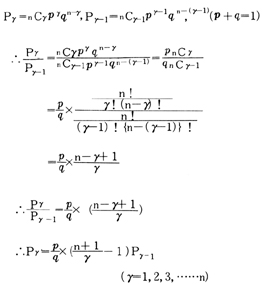
8．ポアソン分布表

　ポアソン分布表も，二項分布表と全く同じように，PγとPγ−1に関する漸化式を用いて作成する。

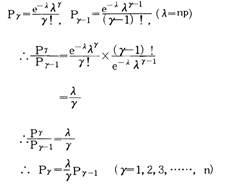
9．正規分布表

　変量Xが，平均値m，分散σ ²の正規分布N（m，σ²）；

に従うとき，変数の変換によってUは標準正規分布N（0，1）；

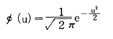
に従うことはすぐにわかる。変数をこのように変換すれば，どんな正規分布も，標準正規分布N（O，1）に変えることができるから，正規分布に関する確率は，標準正規分布について計算しておけばよいわけである。そのようなわけで，

におけるtと，それに対応する確率P（t）の値を表にしたものが，いわゆる正規分布表といわれているものである。ところで，この確率の値を求めるための右辺の定積分は，素直に求まるものではないので，正規分布表の作成は，この定積分の値をいかにして計算するかにかかってくる。
さて，e^xは，次のように展開される。