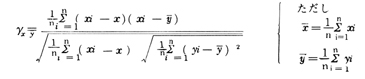研究紀要第38号 学習指導に関する研究 - 073/081page

危険率α＝0．05からχ°（φ，α）≒30，1を得る

�C次の比較により適合の判定を行う。

　χ²＞χδ（φ，α）：適合していない。
　χ²＜χδ（φ，α）：一応適合している。

図5−3に示したのは，度数とχ²を求めるプログラムと，2000個の乱数を検定した結果である。
図5−1の度数ヒストグラムの下方に，乱数適合判定の結果が印字されている。

（2）　系列相関検定

　乱数の無規則性（独立性）を検定するためには，乱数列前後の関連の有無をチェックすればよい。
　たとえば，表5−1の1行1列目から，38　32　19　46　19　42　49…のような数列をとり出し，38と32，32と19，19と46…を，直角座標のPn（xn，yn）点としてプロットすればよい。実際は，2次元配列に（�T，�T＋1）をとり，＊や○でプロットした図を相関図（散布図）という。

図5−4（A）（�T，�T＋1）の相関図
図5−4（B）（�T，�T＋3）の相関図

　このように直角座標にプロットされた状態を見れば，直観的に相関がわかる。図5−4（A）は，乱数1000個をプロットした相関散布図である。この点の散布状況を見ると，直角座標いっぱいにばらついて相関がないと判定されそうである。しかし，これは乱数列の前後の関係で，二つおき，三つおき，四つおき等の場合はどうであろうか。図5−4（B）は，三つおき，すなわち，（xn，yn＋3）の場合の相関散布図であり，（A）図と比較しても両図とも視覚で判断がつくが，これを定量的に判定するには，計算式により相関係数γxyを求めなければいけない。