研究紀要第51号 「学習指導の個別化 個に応ずる研究」 -014/080page

数学の学習についてのアンケート

番号（　　）　　　氏名（　　　　　　　）

このアンケートは，数学の学習についてたずねるものです。テストや成績とはまったく関係ありませんので，ありのまま答えてください。

※	次の1〜5の間いに対して，ア〜工の中から一つ選んで，その記号を○でかこんでください。

1．数学の学習は，好きですか，きらいですか。

ア．好き イ．どちらかといえば女子き ウ．どちらかといえばきらい エ．きらい その理由はどんなことですか。

2．	あなたは，めあて（何を学習するのか）がはっきりわかって授業にのぞんでいますか。

ア．めあてがわかって授業にのぞんでいる イ．どちらかといえば，めあてがわかっていることが多い ウ．どちらかといえば，めあてがわかっていないことが多い エ．めあてがわからないで授業にのぞんでいる

3．	授業が終わったあとで，あなたは，何がわかって，何がわからなかったかを考える（見直す）ことがありますか。

ア．よく考える イ．どちらかといえば考える ウ．どちらかといえば考えない エ．考えない

4．	あなたは，問題などを解いていて，つまずくことが多い方ですか，少ない方ですか。

ア．つまずくことが少ない イ．どちらかといえば，つまずくことが少ない ウ．どちらかといえば，つまずくことが多い エ．つまずくことが多い

5．	あなたは，つまずいたり，わからないことがあった場合どうしますか。

ア． そのままにしておかないで，教科書などで調べたり，先生や友達に聞くなどして解決することが多い イ． そのままにしておくこともあるが，どちらかといえば，教科書などで調べたり，先生や友達に聞くなどして解決することが多い ウ． どちらかといえば，そのままにしている エ． そのままにしている

エ　前提条件テスト

方程式の学習に必要な既習の基礎的な知識・理解，技能が一人一人の生徒にどの程度身についているか，また，クラス全体としてどこが陥没しているかなどを診断する目的で，前提条件テストを実施した。

なお，このテストの結果をもとにして，既習事項について，解けた（○），解けない（×）の2段階で自己確かめをさせ，それぞれに応じためあてをもって学習が進められるようにした。（P16，学習のめあて表の「必要な既習事項」を参照）

前提条件テスト

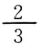
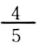
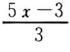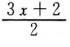
1．次の計算をせよ。 （1）　（−2）＋（＋5） （2）　3−5 （3）　−4−2 （4）　−5＋7 （5）　3−8＋2 （6）　−4＋7−9 （7）　（−4）×6 （8）　（−28）÷（−4） （9）　12÷（−3） 2．次の□にあてはまる数を求めよ。 （1）2÷□＝ （2）□÷10＝ 3．次の計算をせよ。 （1）　6m−m （2）　8y＋13y （3）　−7x＋6x （4）　3x−7x＋x （5）　−3x＋4＋4x−5 （6）　−4（5x−4） （7）　 ×12 （8）　−6× 4．次の□にあてはまる数量を，文字を使った式で表せ。 （1） x gの10％は□ gである。 （2） 時速5 kmで1時間歩いたときの道のりは，□ kmである。 （3） a kmの道のりを，毎時50 kmの速さの自動車で行くと□時間かかる。 （4） xの4倍からyをひいたときの差は，□である。 （5） 十の位，一の位の数字が，それぞれa，5である2けたの整数は□である。 （6） x人の子どもに，みかんを3個ずつ配ったら8個足りなくなった。みかんの数は□ 個である。

オ　事前テスト・事後テスト

方程式の学習の事前と事後に，24ぺ一ジに示した小問15問からなる同一のテストを実施し，それらの結果から，方程式やその解の意味，方程式の解き方についての変容をとらえることにした。なお，事前テストの結果をもとに，その後の方程式の学習内容について，どの程度の知識・理解をもっているかをとらえ，個の特性把握のための一つの資料にもした。

［2］　個別化のための手だて

ア　学習指導カード

［1］で述べた個の特性把握のための調査・検査の結果と，それらをもとにした教師のかかわり方や，毎時間の学習の中で目だった徴候，生徒の自己評価の結果などの概要をまとめ，指導の中での個に応じた働きかけのための指導資料として活用した。その形式や内容については，15ぺ一ジにB子の例で示してある。