研究紀要第51号 「学習指導の個別化 個に応ずる研究」 -016/080pagepage

イ　学習のめあて表

生徒一人一人が，課題意識をもって毎時間の授業に取り組めるようにするため，次のような学習のめあて表を作成した。

これによって，生徒たちは，単元における学習の流れと，毎時間の到達目標をとらえることができ，これまでよりはっきりしためあてをもって授業にのぞめるものと考えた。さらには，授業に必要な既習事項について自己確かめをしながら学習を進めることにより，自分のつまずきを把握し，それを解消するためにそれぞれのめあてをもって学習できるものと考えた。

学習のめあて表

単元の目標

○方程式やその解の意味がわかる。 ○等式の性質や移項の考えを用いて方程式を解くことができる。 ○方程式を用いて，応用問題を解くことができる。

月日	項	到達目標	必要な既習事項
	1　方程式	○数量の関係を，等式を用いて表すことができる。 ・時速4 kmでa時間歩いたときの道のりはb kmである。 ・たてa cm，横b cmの長方形の周の長さはl cmである。 ○方程式やその解の意味がわかる。 ○方程式の解を求めることができる。 ・−2，−1，0，1，2のうち，3 x−5 = x−3の解になっているものを選び出せ。	前提条件テストの結果をもとにした自己確かめ …解けた …解けない 正負の数の計算 ［1］　（−2）＋（＋5） □ ［2］　3−5 □ ［3］　−4−2 □ ［4］　−5＋7 □ ［5］　3−8＋2 □ ［6］　−4＋7−9 □ ［7］　（−4）×6 □ ［8］　 （−28）÷（−4） □ ［9］　12÷（−3） □ ［10］　−7÷2 □
	2　等式の性質と方程式の解き方	○等式の性質をのべることができる。 ○等式の性質の大切なわけがわかる。 ○等式の性質を用いて，簡単な式変形ができる。 ・a + 3 ＝ 5   ○ 　a＝5−3 ・2 x＝−4   ○ 　x＝−2 （○には等式の性質の番号を人れる。）
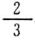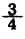		○等式の性質を用いて，簡単な方程式を解くことができる。 ・x＋3＝1 ・x−5＝6 ・−3 x＝9 ・ x＝4 ・ x＝−
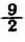
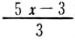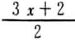
	3　1次方程式の解き方	○移項することの意味や，移項のしかたがわかる。 ○移項の考えを用いて，簡単な方程式を解くことができる。 ・x＋8＝3 ・3 x＝5 x＋4 ○1次方程式の意味がわかる。	文字式の計算 ［1］　6 m−m □ ［2］　8 y＋13 y □ ［3］　−7 x＋6 x □ ［4］　3 x−7x＋x □ ［5］　 −3x＋4+4x−5＝−5 □ ［6］　2（3 x−5） □ ［7］　−4（5 x−4） □ ［8］　5 x−2（x＋5） □ ［9］　 ×12 □ ［10］　−6× □ 数量を文字式で表す ［1］　x gの10％は……□ ［2］　時速5�qでt時間歩くと……□ ［3］　a kmの道のりを時速50kmで……□ ［4］　xの4倍からyをひいた差……□ ［5］　十の位がa，一の位が5の整数……□ ［6］　x人の子どもにみかんを3個ずつ配ったら8個足りない……□
		○次のような方程式の解法手順を説明できる。 ・3 x−2＝5 x＋4 ○手順にしたがって方程式を解くことができる。
		○かっこのついた方程式を解くことができる。 ・5 x−2（x−1）＝14
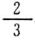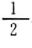		○係数に少数をふくむ方程式を解くことができる。 ・1．2 x−3＝0．5 x＋1．9 ○係数に分数がある方程式を解くことができる。 ・ x＋2＝ −3
		○係数に分数がある方程式を解くことができる。 ・ 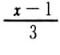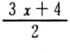− ＝−7
		○いろいろな形の方程式について，自己評価票の結果などをもとに，自分のつまずきやできぐあいに応じためあを作り，それに到達できる。 私のめあて
	4　1次方程式の応用	○応用問題を解く手順がわかる。 ○手順にしたがって，簡単な応用問題を解くことができる。 ・1個70円のりんごと，1個50円のなしをまぜて20個買い，1260円支払った。りんごは何個買いましたか。
		○いろいろな応用問題を解くことができる。 ・数に関する問題 ・時問・距離・速さに関する問題　など
	演習	私のめあて