研究紀要第51号 「学習指導の個別化 個に応ずる研究」 -025/080page

校の1年7組の生徒に対して定めたおおよそのめあてであることを付け加えておく。

表2は，1学期の数学の評定をもとに，クラスの生徒全員を上位群（11名），中位群（18名），下位群（13名）の3群に分け，各群ごとの有効度指数などを示したものである。これによって，各群の定着の傾向をみようとした。

表2　事前・事後テストの結果（その2）

問題番号		区分	正答率％		有効度指数		問題番号		区分	正答率％		有効度指数
			事前	事後						事前	事後
1	（1）	上 中 下	36 39 8	91 72 38	86 54 33		3	（4）	上 中 下	36 17 8	100 100 100	100 100 100
	（2）	上 中 下	45 17 0	73 78 23	51 73 23			（5）	上 中 下	0 0 0	100 100 77	100 100 77
2	（1）	上 中 下	0 0 0	100 94 77	100 94 77			（6）	上 中 下	0 0 0	82 94 54	82 94 54
	（2）	上 中 下	0 0 0	100 100 85	100 100 85			（7）	上 中 下	0 0 0	100 89 62	100 89 62
	（3）	上 中 下	0 0 0	100 100 77	100 100 77			（8）	上 中 下	0 0 0	91 78 69	91 78 69
3	（1）	上 中 下	64 72 38	100 100 100	100 100 100			（9）	上 中 下	0 0 0	55 61 38	55 61 38
	（2）	上 中 下	27 6 8	91 89 46	88 88 41			（10）	上 中 下	0 0 0	64 22 15	64 22 15
	（3）	上 中 下	36 39 15	100 83 38	100 72 27		平均		上 中 下	16 13 5	90 84 60	88 82 59

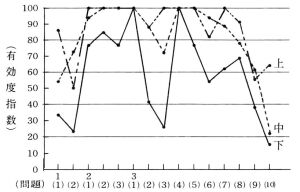
上の表から次のことがわかる。

○	3群とも有効度指数が60以上の問題は，2の（1），（2），（3），3の（1），（4），（5），（7），（8）の8問で，1次方程式の基本的な問題は解けるようになったといえる。
○	下位群が他の2群と比較して，有効度指数が特に低い問題として3の（2），（3），（6），（9）があげられる。これらの問いは，係数が分数であるか，または，解が分数である。下位群の生徒には，分数に抵抗がみられる。
○	中位群の有効度指数が上位群のそれを上回る問題は，1の（2），3の（6），（9）である。

［2］　S-P表による考察（事後テスト）

前提条件・事前・事後の各テストの結果については，当教育センター情報処理教育係で開発したプログラムにより，マイコンを用いてS−P表を作成した。これによって，クラス全体の得点および一人一人の生徒や個々の問題の特性を視覚的に，また計量的にとらえようとした。

表3は，事後テストの結果のS−P表である。表中のSNOは生徒の出席番号を意味し，その下に得点の高い順に生徒を並べ，また，PNOは問題番号を意味し，その右側に正答率の高い順に問題を並べた。また，○は正答，×は誤り，・は無答を示す。例えば，出席番号19番の生徒が誤った問題は3（10）のみ，無答が3（2）ひとつだけで，他の問題は正答したことになる。

このS−P表から次のことがいえる。

○	全体的にみた場合，正答率80％以上の生徒が28名（67％）と高得点者が多い。しかし，7名の生徒は，正答率50％に達せず，「1次方程式の解き方」について目標を達成したとはいえない。なお，この生徒たちは，前提条件テストの正答率が52％から24％の間であったので，特に個別指導の機会を多くしてきたが，更に継続する必要がある。
○	注意係数（C・S）は，クラス平均で0．20（上位群0．20，中位群0．16，下位群0．25）と比較的小さく，0．5以上の生徒は4人であった。注意係数は，全体の得点パターンの傾向に対して，異質な得点のとり方の程度を定量的に表した数値で，0．5以上のときは要注意，0．7以上のときは特に注意して検討すべきであるとい