研究紀要第63号 「教育課程の実施に関する研究」 -059/093page

（3）授業における指導の実際
　ここでは，証明指導のための第二段階の証明の必要感を持たせる指導と第三段階の証明を口頭で述べさせる指導の実際例を述べることにする。

1　証明の必要感を持たせる指導例

課　題 ∠Aが60度である△ABCがある。この三角形で∠Bの二等分線と∠Cの外角の二等分線の交点Pの∠BPCの大きさを求めよ。

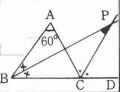
　指導のねらいは，三角形の内角や外角についての性質や関係を理解させ，それを用いて証明の必要感を持たせることである。まず，問題を提示し，ノートに正確な作図をさせる。授業は全体の討議形式で，自由に発表させる。
　T　「さて，∠BPCは何度になると思いますか。」
　Pl「30度だと思います。」
　ほとんどの生徒は，図から直観で求めているはずである。そこで，その理由を考えさせる。
　T　「本当に30度になるのかな。だれかにその理由を説明してもらいたいですね。」
　P2「（黒板の図で）こことここが半分だから，Pのところも∠Aの半分になると思うから30度になると思いました。」
　P3「30度と予想して三角定規の30度の角を当てたらぴったしだったからです。」
　P2の説明では，図にある文字を使って，「∠ABCと∠ACDが二等分になって……」などの言い方についても軽くふれておく。P3の実測については，論理的な説明を要求しているときなので軽視されやすいが，実験・実測の大切さにも留意させながら，さらに，発問する。
　T　「P3さんの方法は，∠Aが70度ではどうですか。」
　P4　「60度のときしか使えないです。」
　∠Aの角度を変えた問題や角度を明示しない問題を出して，実験・実測の限界に気づかせることによって，証明の必要牲を感じさせることのできるところである。
　P5　「先生，P2君の説明はなんかスキッとしないのですが，もし，P2君の説明が正しいとすれば，と∠ABCとと∠ACDを3等分すれば∠Pは∠Aの1/3になるのですか。」
　T　「P2君，P5君はあなたの説明では納得できないでいるようだが，どうですか。」
　P2　「………」
　ここで，30度になる証明と一般化した∠P＝1/n∠Aの証明の学習活動が展開されることになる。
　このように，本人には別に証明の必要を感じない事柄も，他人には納得できない点を指摘して，これをとりあげ，問題点を分析し，整理しながら証明の必要性を理解させていくことが，これからの証明の学習意欲に大きく影響すると考えられるので，十分な指導をしておくことが必要であると思われる。
　なお，必要感を持つような課題を選ぶときは，生徒がなんらかの手段で結論を予想しやすいもので，その結論に対して，「どうして言えるのか。」「いつでも言えるのか。」という疑問に発展する課題であることが大切である。

2　証明を口頭で述べさせる指導例
　この指導例は，P.DlOの学習指導案による授業の実際である。生徒の主体的学習活動の場を位置づけた学習内容・活動の3の2人組で証明をつくりあげるところと4の証明を口頭で発表するところである。
　証明を口頭で述べさせるねらいは，まず，証明を書くという負担を生徒から取り除き，普通の話し言葉で正しい推論ができることに力点をおくためと考える。証明の正しい筋道がわかって，相手を納得させる表現ができれば，証明ができる喜びにもなり，証明の記述にもスムーズに入れると思われる。
　さて，生徒は，仮定から結論までの筋道を考えるのに，教科書等に例示された証明のような順で考えるものと思っているものが多い。そこで，次に図示するような結論から考えたり，仮定に戻っ