研究紀要第101号 「学力診断テスト開発に関する研究」 -015/170page

乗法計算でもその計算力をみることはできるが,計算をするうえで必要な約分が3回入るような数値を工夫し,3口の計算とした。これにより,「表現・処理」の観点から処理できると考え,(2)の分数の除法についても同様に3口の計算問題を取り入れるようにした。
　(4)の分数,小数の混じった計算については,小数を分数に直して処理することだけに限らず,分配の法則を活用すればより簡単に計算することができる設間とし,それに着目して処理できる力をみることができるように工夫した。
　また,各小間ともに,児童の傾向等を細かく分析し,約分でのつまずきなどを想定して5つの選択肢を設定するように配慮した。

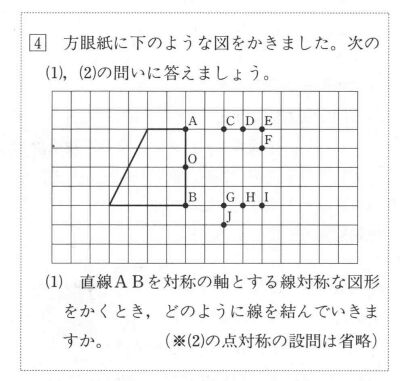
　「図形」領域の「線対称・点対称」に関する設問である。この領域に関する「表現・処理」の能力をみる方法の一つとしては,実際に作図をさせる方法がある。しかし,コンピュータによる処理をするために作図をさせることには困難な面がある。また,能力を細かく分析するためには,単に作図の結果だけではなく,その過程をみる必要がある。
　そこで,設間にあるように対称な図形を作図をするためには,必要な点をどのように結んでいけばよいかを考えさせ,手順や方法がわかって正しくかけるまでが技能化されているかをみられるような形に設問を工夫した。

(2)　中学校第2学年
　数学2年では数学的な表現・処理をみる問題として第2部の[1](1)〜(3)では簡単な単項式と多項式の四則演算の力を見ようとしている。特に一(多項式)の形のときは−1X(多項式)として括弧をはずす際の符号の変化について考えられるかを見ている。
−(7−2)＝−5と−(7−2)＝−7＋2＝−5が等しい結果になることを確認するなど計算の原理が身に付いているかを求めている。(−a) ³ の符号についても,累乗の指数の計算が処理できるか,同じ文字どうしの約分が理解されているかが問えるように設定した。
　s＝(a＋b)/2をaについて解く間題には,両辺の入れ替え,移行,両辺への乗除の仕方等の行い方や順序が正確でないと求められないように出題してある。回については,二等辺三角形の持つ性質が理解されているかが問われる。これは第1部の[7]の(1)(2)の理解と関連が深い。しかもこの[5]や[6]は角の二等分線を加えて問題を設定し,用語として知っているだけでなく,底角の二等分線を加えて複合的に思考できているかをとらえようとして設問している。
　更に[6]では三角形ABCの∠Bと∠Cの二等分線の交点をIとして∠BICの角度を∠A=5ぴの条件で求めさせている。これは直角二等辺三角形の合同条件が証明に使えることを含め,三角形の3つの内角の二等分線は1点で交わるなども使えるし,頂点Aと点Iを結ぷ直線を引きその延長線と辺BCとの交点をつくれば三角形ABIと三角形ACIのそれぞれの内角Iの外角の和をも使えるというふうに多様な考え方が可能なものとしてある。
　[7]は相似な図形で,1組の対応する辺の長さから相似比を求めたり,相似比を使って対応する辺の長さを求めることができるかをねらって出題しているので,まずは相似な図形を選びだせるか,三角形の相似条件を利用できるかが間われる。そうでないと対応する辺や対応する角が見いだせないことになる。
　ここでは△ABC∞△DAC∞△DBAがあるので,どれとどの三角形で考えるかの幅にも含みをもたせてある。△ABC∞△DBAでも考えられるが