研究紀要第101号 「学力診断テスト開発に関する研究」 -016/170page

この組み合わせを選ぷとかなり複雑化するし,時間もかかるので,回答は選択式に設定しておいた。
　[9]も相似形に関する性質を用いて,未知の長さを求める問題であるが,AB:BC=3:2のときにBD:CEも3:2と考える誤りが多い。

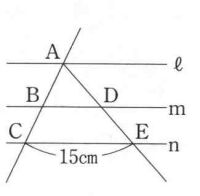
相似形に関する性質を用いて,未知の長さを求める問題

　これも,相似の三角形を具体的におさえて,対応する線分を正確に確認できれば問題がないが,表現・処理の過程て常に三角形の相似条件を基本においた指導ができているかがポイントとなろう。
　[8]は,正三角形の外角を使って頂点の数を求める問題だが,内角・外角の意味,多角形の外角の和,n角形の内角の和など総合的問題として出題した。
　10．と11．は一次関数の式をグラフに表すことができるかを見ようとした間題であり,一方は2組のx,yの値が与えられたとき一次関数の式が求められるかどうかを見るために,他方は具体的ないくつかの一次関数のグラフの中から,条件にあうグラフが選択できるかなどを見るために出題してある。
　y=ax+bのaが傾き1/2,bがy切片−1を表していることの理解ができれば,グラフの選択は容易である。しかも1年での一次方程式での学習が生かされれば,1組のｘ,yの値はグラフの交点を読み,具体的に代入して確かめることも可能であろう。何よりも,一次関数の式を決定するには,何と何がわかればよいのかを考えさせ,「変化の割合と1組のx,yの値(傾きと1点の座標)」「2組のx,yの値(1点の座標)」がわかればよいことというようにしたいものである。
　2組のx,yの値をy=ax+bのx,yに通過点を代入して連立方程式で求めることができることをグラフとの関連で理解できているかが大事になってくる。このように10．と11．を同時にみると一人一人の生徒の変化や対応についての見方や考え方の深まり具合が見えるだろうし,関数と,一般に表現されるax＋by=cの方程式も同じ直線のグラフに表現できることなどへも発展できる。

4　信想性,客観性を持たせるための工夫

　各部の設問に際しては,それぞれの学年の作成者が予想した正答率と予備調査等の正答率を比較検討し,その差が大きいものについては,修正・改善を行うなどして対応した。
　主な内容としては,数値等の変更による間題内容そのものの修正と選択式から記述式への出題形式の変更等を行い,信憑性,客観性を持たせるための工夫をした。具体的には,次のようなものである。
○ 第5学年用　第1部(知識・理解)
〈数値を変更した間題〉

［1］次の（　）の中に、あてはまる数はいくつですか。 　725×3.4＝725×34÷（　）

　1部の最初の設問ということもあり,十進法の仕組みを問う基本的な間題として,「72.5×3.4」を考えた。しかし,予備調査の結果から乗数・被乗数ともに小数という点が正答率が低い原因ととらえ,乗数のみを小数とするように改めた。
〈出題形式を変更した問題〉

［6］次の（1），（2）にあてはまる数は何ですか。答えは、解答用紙に数字で書きいれ… 　　（1）（4，8，12）の最小公倍数 　　（2）（3，9，15）の最大公約数

　この設問の場合には,他の問題のように選択肢を設けてしまうと,倍数と公倍数の関係,約数と公約数の関係などに着目して考えずに,選択肢にあげられている数値をもとに推測で解答してしまう児童が見受けられる。
　そこで,出題形式を選択式から記述式に変更するようにした。つまり,3つの数の最小公倍数を求めるためには,一番大きな数に渚目して考えることや,最大公約数の場合には,一番小さな数に着目し,その約数をもとに考えることへの理解等をみることができるよう配慮し,客観性を高めた。