研究紀要第123号 「学力向上のための授業改善に関する調査・実践研究」 -021/076page

中学校数学

1　研究の視点

　平成9年度に実施した学カ到達度調査より，「1次関数」の中領域が低いことが分かった。本研究では，中学2年の「1次関数」を中心としながら，他の学年の関数領域についてもとりあげ，以下の4つの視点で実践した。

　ア 図などとの関連により，]次関数の式を理解させる。
　イ 対応表・グラフ・式の相互関連を図った指導をする。
　ウ 関数指導にコンピュータを活用する。
　エ 系統性を踏まえた指導をする。

2　実践研究

　（1）「1次関数の指導」について(視点ア・イ)
　教科書にある問題を次のように変え，提示した。

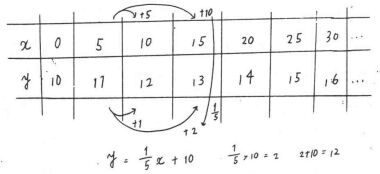
ばねののびは，下げたおもりの重さに比例する。 いま，lOgのおもりを下げたときのばねの長さがl2cmであり，30gのおもりでは16cmであるとする。

　初めに生徒―人―人が自分なりにこの事象を把握し，それを図に表現する活動を取り入れた。その活動のあと，全体で確認する時間を設け，不足した部分等を付け加えるようにした。

　この図をみながら，何と何が関数関係であるかを見付けた。そして，本時は「おもりの重さとそのときのばねの長さ」に着目し 「xgのおもりを下げたときのばねの長さをycm」として，この1次関数をいろいろな方法で表現するという課題で展開した。lつの方法で表現したら，別の方法も考えてみるように促した。自カ解決した後，それぞれの考えを発表した。そして，式，グラフ，対応表，そして，図とを比較しながら，それぞれの表現方法の違いや特徴について話し合った。これらの活動を通して1次関数の式について理解させた。
生徒が考えた例

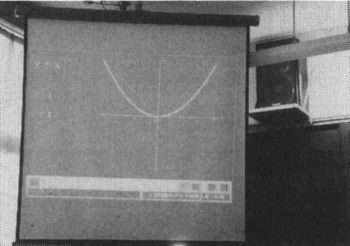
　（2）「2乗に比例する関数」の指導について　(視点ウ)

「y = x ² 」をグラフで表すことを課題とし，実際に対応表に必要な値を入れ，座標に移し替える作業をした。生徒のかいたグラフで多かったのは原点付近とがったグラフであった。さらに細かくxとyの値をとり，原点付近の様子をかき，この段階で，コンピュータを活用し，「y = x ² のグラフ」(原点付近の様子)を示した。原点付近もなめらかな曲線であることを確認しはじめにかいたグラフを修正した。そして，全体のグラフを投影し，特徴をとらえさせた。(使用したソフトは「シミュレーション総合編3年(東京書籍)」)

　（3）小学校6年・中学校]年の「比例」の指導について(視点エ)

　1　小学校での関数指導について
　　　― 小学校6年「比例」―

　「比例」の単元の中の，特に，導入，そして終末はどうあればよいかについて，次の実践をした。

　ア　単元の導入
　導入において，「自動車が家に向かう様子」「誕生日のケーキにろうそくが立っている様子」の絵を提示し，「何かが変わると，別のものも変わる」ものを見付けた。それを「増えると増える」と「増えると減る」の2つに仲間分けをした。さらに，児童は身のまわりにもこの2つの関係があると考え，それを見付ける活動をした。それぞれの関係を付箋に書