福島県教育センター所報ふくしま　No.6（S47/1972.6） -008/025page

それを基礎資料として検討し，46年５月，対象校36校，対象人員6200名の無作為抽出によって本調査をおこなって標準化したものである。また作問にあたっては，テストのねらいが達成されるように，つぎのことを特に考慮して，テスト問題の妥当性と信頼性を高めるように配慮した。

（1）当該学年で学習すべき算数科の内容について，基礎的能力をとらえうるようにしたこと。

　学習した結果の学力の実態をとらえうるという観点から，学習内容の習得の程度を算数科の学力のひとつの内容と考え，その学習内容は学習指導要領に示されている指導内容であるという立場をとった。この指導要額に示されている指導内容の習得の程度をは握できるように，指導要領および教科書の分析をおこない，問題の作成および構成を考えた。

(2) 応用カをとらえうるようにしたこと。
　　学習した知識をもとにして，より発展的に適応する能力，一般的な問題の解決力。さらに統合，拡張する能力など，新指導要領のねらっている算数科における能力をもとらえうるよう配慮した。

(3)　理解の深さおよぴつまづきの箇所を診断できるようにしたこと。
　概念や原理，法則あるいは計算および基礎的事項についての理解の程度の深さ，そして，つまづきの箇所をとらえ，指導に役立てるように，問題の内容および系列等にくふうをして，学習の結果を診断的にとらえうるように配慮した。

(4)　当該学年の算数科の学力について，概観的に，かつ，教科内における学力の差異をも診断的にとらえられるようにしたこと。

　学力を概観的に，診断的にとらえるようにするには，学力の意味内容を規定し，その学力の分野・領域を細分して，それらの領域・分野のねらいにあった内容についての問題を網ら的にもれのないように作成し，構成することによって，テスト問題としての妥当性が高められ，学力を概観的にかつ診断的にとらえうるように考慮した。

　ここにおいて，学力の規定は，つぎの２つが考えられる。
　１　経験（内容）領域による方法
　　「数と計算」「図形」‥‥‥などのように生活経験・内容によって分ける。
　２　能力概念領域による方法
　　「知瀬・理解」「技能」「態度」などのように，能力としてとらえる。

　問題の作成にあたっては，上記１，２の両者を加味した分類による方法を用い，算数の学力を診断的にとらえるテスト問題として妥当性を高めるように意を用いた。
ここで教科内の学力の差異は学力の１の分類による，経験（内容）領域による差異をとらえるようにした。以上のことを基本として，領域の設定，問題の内容，および小間数を考え問琴を作成した。

　３　テスト問題の領域の設定について

　前述の問題作成の基本方針から，領域は学習指導要領に示されている指導内容についての領域をそのまま用いるのが適切であると考えられる。新指導要領では，４領域にわけてあるが，数と計算に関する指導内容の量が，他の領域に比して多く，かつこの領域では，数と計算の意味・理解と計算技能とが考えられるので，この
「数と計算」の領域を二分して，「数と計算の意味」，
「計算」の２つの領域を設け基礎的な能力を診断できるようにした。したがって，
　○数と計算の意味
　○計算
　○量と測定
　○図形
　○数量関係
の５つの領域・分野からなる問題構成をした。

　４　結果の概観

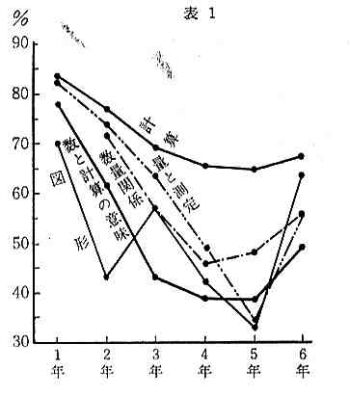
領域別，学年別にみた場合，「図形」領域の正答率が全般的にもっとも低く，１年，３年，６年を山とし，２年，５年を谷とする，Ｗ字型をしめしているのにくらべて，他領域は，５年，４年を谷とするＵ字型分布をしめしている。 (表１参照)
　「計算」領域だけは，最低正答率が，５年の65.15％で，１年の84.2％を最高とする�X字型分布である。とくに，５年の正答率は５領域のうち「計算」領域を除いた４領域が平均正答率50％をわっている。
表１

　　全体の分布型から，３年，４年，５年の全領域が，分布型の谷になっているが，これは，今後の指導面に多くの問題点をかかえていると推測できる。これを指導内容面からみると，具体から抽象化への移行の時期でもある算数科特有の問題であり，より指導法の改善工夫が必要である。またこの分布型を，本調査実施の時期からみると，46年５月という，新指導要衝のスタート直後で，児童にとっては，新指導要領のための移行期での学習であったことの因子も考慮する必要があると思われる。

　５　領域別の概観