福島県教育センター所報ふくしま　No.11（S48/1973.6） -016/025page

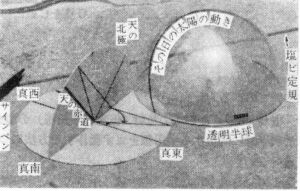
図３　透明半球の内側に半円板を組みいれて,その日の太陽の日周運動経路を求める。

した場合の日の出の方向になる。
なお,ＰＱ線は真東の線である( ＴＰＱは直角)。図２,５（マル５）の図はＡＢＣ半円板を横から見た図である。Ａ面には天の赤道と北極星の方向などがすでに記入してあり,Ｂ面には日の出の点Ｏが記載してある。このＢ面のＯ点を図５（マル５）のようにＣ面と背合せにすることにより,Ｃ面の円弧上に移すことができる。ＢＣ面を広げた図が６（マル６）であるが,Ｃ面のＯ'の点がＢ面のＯ点を移した点である。すなわちＯ'点は目の入りの点になる。なお,ｃ ^。 は日の入りの点の方位角,ｄ ^。 は日の出の方位角,ｅ ^。 は日の出と真南の方向との角度,ＲＰＱは東西方向,ＴＰＵは南北方向を表わしていることになる(方位角の表示法は, ｃ ^。 , ｄ ^。 のように真南から右まわりに表わすのが普通であるが,場合によってはｅ ^。 のように左まわりに表示することもある)。以上のように半円板上で種々の事象を考察できるが,この半円板と透明半球を組みあわせると前述以外に, 太陽の日周運動の経路や,天の赤道 なども透明半球上にプロットできる。
　すなわち,図２の１（マル１）〜６（マル６）での作図の結果できあがった半円板を図３のように透明半球内に内接することにより,半球上にｍ点(南中時の太陽の位置)とＯ点(日の出の位置)と Ｏ'点(日の入りの位置)の３点記載し,この３点をうまく通るような線を引く(この場合幅３mm,長さ３cm位,厚さが 0.5mm 位の塩化ビニル板を定規とすれば,極めて正確な線が引ける),これがその日の太陽の日周運動の経路となる(図３参照のこと)。また,図２,６（マル６）のＱＲ(西点,東点)と,図２,３のm'点(天の赤道)の3点を半球上にプロットして,前述の太陽の日周運動と同様の方法で記載すれば天の赤道が得られる。

(3)観測で得た太陽日周運動経路と半円板で得た日周運動経路との関連

　この両方法による結果は理論的(作図上,あるいは測定上の誤差をのぞけば)には,同じ日については,まったく一致する。一方,探究の過程の中では,これらを効果的に使い分けなければ,科学の方法を無視する結果となる。
　筆者は,これを次のような意図で使用したいと考えている。即ち,科学の方法では,まず観測を実施し(この場合は透明半球を使用し,太陽の日周運動を実際に観測する),データを集めることが重要である。ついで,それをもとに学習が進められるわけで,その時に別の多くの資料が必要になる。そのための資料を教師が実際に時期を変えて,太陽運動の経路を半球上に観測記載したものを準備しておくことは容易でない。そのために前述の方法で簡単に,年間を通して,いかなる時期の太陽運動の経路を半球上に,表記できるとすれば,極めて効率的な学習が展開できるものと考える。

図4半円板(自作)と透明半球
(図３のようにして半透明上に太陽の日周運動経路を記入したものを、とりはずしたところをしめす。)

　また,高等学校においては,生徒自身に持たせ(半円板)その意味を思考しつつ,作図を進めていく中で,天球の概念や,天球上の種々の恒星の運動の意味を理解することができよう(半円板を生徒個人に持たせ,学習する場合には画用紙でもじゅう分所期の目的を達成することができる)。

4. おわりに

　ウエット・ラボとドライ・ラボをタイトルにあげたが,あくまでも,目的に沿った観測,観察データを進めることによって学習が始まるということである。そこに,いわゆる必要な多くのデータ(既有の)を与え,効果的に推論できるような場を与える学習形態も忘れてはならないと思う。また,高等学校地学などにおいてはそうした個人では収集できない,いわゆるグローバルな大きなスケールの学習の対象が必要になってきたことでもドライ・ラボの位置づけが重要になってくると思われる。