福島県教育センター所報ふくしま　No.13（S48/1973.11） -007/026page

したがって，

で与えられる。

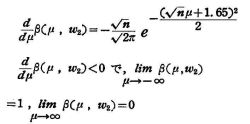
ウ　H ₁ ; μ> 0の場合

　　棄却域は， と定まる。

　したがって，

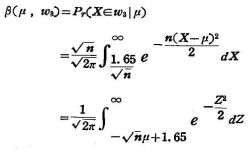
で与えられる。

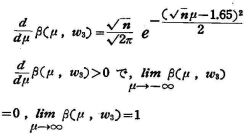
ア，イ，ウを図示すると，次のようになる。

これらの検定力関数のグラフの概形を，n＝16としてかいて，第一種の過誤をあらかじめ指定した（0.05）検定から，第二種の過誤をできるだけ小さくするような検定を選んでみよう。

μ	-0.3	-0.2	-0.1	0	0.1	0.2	0.3
β(μ , w 1 )	0.223	0.126	0.069	0.05	0.069	0.126	0.223
β(μ , w 2 )	0.326	0.198	0.106	0.05	0.020	0.007	0.002
β(μ , w 3 )	0.002	0.007	0.020	0.05	0.106	0.198	0.326

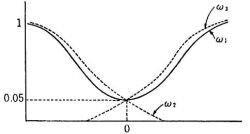
このグラフから，μ<0だけを考えるときは，β(μ , w ₂ ) > β(μ , w ₁ )であるから検定ｗ ₂ を採用すればよい。μ> 0だけを考えるときは，

β(μ , w ₃ ) > β(μ , w ₁ )であるから検定ｗ ₃ を採用すればよい。μ≠0を考えるときは，

μ<0ならば，β(μ , w ₂ ) > β(μ , w ₁ ),　β(μ , w ₁ )> β(μ , w ₃ )であり，μ> 0ならば，β(μ , w ₃ ) > β(μ , w ₁ ),　β(μ , w ₁ )> β(μ , w ₂ )であるから，すべてのμ≠0に対して最強力検定は存在しない。

この最強力検定が存在しないときは，どのような不偏検定の考えと発展する。

そして，その結果として，両側検定が望ましい検定であることが知られる。

4　おわりに

ここまでの考察から，基本的な考え方についてまとめると，次のようになるであろう。

(1)　偶然変動の考え方

偶然変動の数学的表現としての確率分布の考えがすべての点に関連する。

　

(2)　有意水準の考え方

有意水準と偶然変動との関係から，棄却域を定めてくる考えは，発展的な考察であり処理であろう。

　

(3)　過誤についての考え方

第一種の過誤と第二種の過誤との関係から導かれる検定力関数の考えは，Neyman，Pearsonの考えを説明するのに役立つ。

そして，Neyman，Pearsoの考えには，統計的なものの見九とらえ方の数学化をみることができよう。