福島県教育センター所報ふくしま　No.16（S49/1974.6） -013/025page

この壷の中から大きさrの非復元無作為標本を抽出するとき，標本の中に入っている赤球の個数をxとし，そのときの確率変数をXとする。」

このとき，

であって，

関心の結果空間は

かつxは整数｝である。

このようにして定義される確率modelを超幾何分布という。

確率変数Xの平均は，E(X)=rm/(m+n)で，Xの分散は，

である。

（2）最尤推定値

壷の中に入っている球の総数はt=m+n未知数であるが，赤球の数mは既知数であるとして，tを標本調査の結果によって定めてみよう。

そこで， (t)=Pr(X=x)とおき，xを固定し，tを動かして (t)を最大とするtの値を求める。

(t)/ (t-1)=(t-m)(t-r)/(t-m-r+x)tを調べると，tx＜mrのとき， (t)＞ (t-1)で，tx＞mrのとき， (t)＜ (t-1)となる。

これは，tの増加にともなって系列 (t)は最初増加し，その後減少することを意味する。

したがって， のとき (t)は最大となる。

i.e.大きさrの標本を抽出して標本調査を行った結果，赤球がx個出現したとすれば，このような結果を最も大きい確率によってもたらす母集団の

大きさtは， である。

そこで， によって確定したtの値を で表わし，これをtの最尤推定値という。

（3)　例題

再捕獲の資料から動物の集団の数を推定する問題を考えてみよう。

「湖で獲った1000尾の魚に赤印をつけて放してやるとする。しばらくの期間をおいて，新たに1000尾を捕獲したところ，その中に赤印のものが100尾いた。この湖の魚の数についてどのような結論が得られるか。」

当然，2回目の魚の捕獲は湖の中のすべての魚からなる母集団からのrandomな標本と考え，2回目の捕獲までの期間中の魚の数は変わらないものとして，問題を一般化する。

湖の中の魚の数をt（未知数），最初に捕獲した魚の数をm，2回目に捕獲した魚の数をr，2回目に捕獲したときの赤印の魚の数をxとすると，2回目の捕獲にちょうどx尾の赤印の魚が含まれる確率は (t)となる。

したがって，超幾何分布を適用すれば，tの最尤推定値は となる。

しかし，実際に湖に棲息している魚の総数はちょうど10000尾であるとは限らない。

そこで，tがその中に入っていると合理的に期待し得る範囲を求めるのが普通である。

確率の計算に，次の中心極限定理を応用する。

「X ₁ ，X ₂ ，・・・，X _n ，が独立な確率変数であるとき，Y _n =X ₁ +・・・+X _n とおくと である。」

ここでは，標本を1尾ずつ抽出するものとして，第i回目の抽出によって赤印が選ばれたとき，X _i =1，そうでないときX _i =0とすると，tやmが大きいから，確率変数X ₁ ，X ₂ ，・・・，X _n を独立であると考えてよいであろう。

t=8500，m=r=1000とおき，2回目の標本に赤印の魚が100尾以下である確率を求めると，

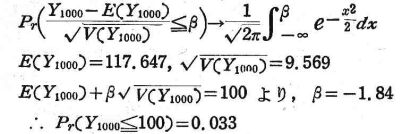
次に，t=12000，m=r=1000とおき，2回目の標本に赤印の魚が100尾以上である確率を求めると，

より，

このことは，魚の数tは8500＜t＜12000であることを正当化するものであり，そして，この結論に対する信頼度は約94％であることを示す。

4．おわりに

ここまでの考察から，現象を数学的な考察・処理にのせていくときの教材展開についての留意点をplotすると，次のようになるであろう。

　<1> 現象を理想化する意味について考えさせ，理想化によって現象の記述が可能になることを理解させるようにする。

　<2> 標本点の重さの与え方を，実験によって一般的な方向づけをし，理論的規約として，その重さを導入することの意味が理解できるようにする。

　<3> 関心の結果空間に確率測度を誘導して，確率modelを求めさせ，その求めた確率modelが考えている偶然変動をうまく記述しているかどうかを考えられるようにする。

　<4> 確率modelを用いて，一般的傾向を推測し，その推測結果の信頼の程度を求めることができることも知らせるようにする。

次回は，この検討結果にもとづく教材展開についてふれてみたい。