福島県教育センター所報ふくしま　No.28（S51/1976.10） -017/026page

して効果があがるかということについては今後の研究課題である。

　2　事後テストの例

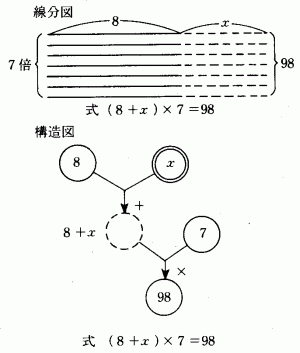
　問題：8にある数をたして7倍したら98になりました。ある数はいくらでしようか。

　出題意図　2段階思考の問題をXを使って式に表わして解かせる。

　3　検　定

　実験群と統制群に事後テストを実施して，次のような結果を得たので2標本順位検定法により検定をした。

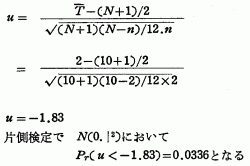
　∴　有意水準5%で仮説は棄却される。よって実験群に実施した訓練の効果は認められる。

　4　結　論

　文章題を解かせる場合に線分図や情景図などを用いることが多いけれども，5年の「問題の考えかた（1）」　においては構造図を用いて指導した方が，問題を解決するにあたって，数量間の相互関係がとらえやすいのでより有効な手段と推測される。

5．反省と問題点

　（1）　積造図に関する指導は，低学年より計画的に導入した方がより有効であるように思われる。

　（2）　構造図のかき方のきまりは，学枚や学級の実態に合わせて，弾力的にあつかう必要があろう。

　（3）　構造図による解き方を万能と考えないで，問題に応じて活用したいものである。

　（4）　これまでの研究をもとにして，今後もこれを続継し，よりよい効果的な指導をしていきたいものである。

6．参考文献

　（1）算数数学の構造式

　　　萩野忠則著，東洋館出版社

　　　　「構造図という思想」

　（2）問題解決の指導

　　　戸田　清，和田義信監修　金子書房

　　　「指導上の問題点と構造図による対策」

　（3）「愛媛大学記要」　第5部　第13巻　第1号

　　　　越智政雄著

先生方の研究物を収集中!!
当センターでは，収集した図書・資料・情報を提供し，枚内研修やグループ・個人研究に役立たせていただいております。 　資料・情報の収集・提供の重点の一つに，県内の先生方や学校・研究会等でまとめられた研究物があります。 　幸い多くの方のご理解ご協力により徐々にご寄贈の数も多くなりつつありますが，まだまだ収集もれの資料が相当数あると思われます。 　本県の風土から生まれた文献は，教育研究・実践の適切な資料であり，貴重な遺産でもあります。 　仲間の方々や近隣の学校・研究会等で研究物がまとまったとの情報を得られましたら，お手数でもご連絡くださるようお願いいたします。