福島県教育センター所報ふくしま　No.30（S52/1977.2） -009/025page

　同正答率の小問の場合は，各々の小問の1に対応する児童の合計得点の高い順にならべることになる。能率的な処理の面から考えると，0に対応する児童の合計得点の低い順にならべても同じ結果になる。

　3（丸囲み数字）5（丸囲み数字）6（丸囲み数字）の小問は同正答率なので，ならべる順序を決定してみる。三小問とも1より0の数が少ないので，0に対応する児童の合計得点を算出し，小さい順にならべるのが能率的である。3（丸囲み数字）6＋6＋4＝16　5（丸囲み数字）5＋4＋4＝13　6（丸囲み数字）5＋4＋3＝12　結果から6（丸囲み数字）5（丸囲み数字）3（丸囲み数字）となる。

○　S曲線とP曲線

　S曲線⇒学習成果の到達水準，得点の累積分布状況を全体的，統計的に観察するための曲線で，各々の児童について，左から得点の数を，かぞえていれた区切線を結んだ曲線である。（正答数7つのものには，左からかぞえて，7つめと8つめの間に区切り線を入れる）

　P曲線⇒問題の正答率，累積分布状況，困難度等を，全体的，統計的に分析するための曲線で，年々の問題について，上から正答者数を，かぞえていれた区切線を，結んだ曲線である。（小問の正答者数8人のときは，上からかぞえて，8と9の間に区切り線を入れる）

3．S−P表の観察，分析，，解釈の基礎

（1）観察

　観察の第一は，表全体の反応パターンをみることである。両曲線がどんな型にえがかれたかを読みとる基礎として，代表的なパターンの特徴，性質をおさえておくと実際にS−P表を作成し，活用する時に役立つ。

　代表的なパターンとしては，テスト型，演習問題型，ドリル型，プログラム学習型など4つのものが考えられているが，具体的には所報23号を参照していただきたい。

　通常　S曲線とP曲線は一致しない。両曲線のズレのおこる原因として，次のようなことが考えられている。

・問題群の中に異質的（問題を解決するのに，いくつもの異なった能力を必要とするよう構成されている）な小問が混入したりしている場合

・指導とテストをするまでの，へだたりが大きく，学習者に忘却現象がおこっている場合

・学習者のモチべ−ションが変化した場合

・学習者が，いろいろな理由から，コンデションが，不良になっている場合

・ドリルが不十分で，学習内容が十分定着せず，不安定になっている場合

・問題の発問等が不明確である場合

（2）分析と解釈

　-1-　S−P表を授業分析に生かすための定量的分析

　<ア> 差異係数⇒SとP両曲線のズレの程度を定量化した係数で，次の式でもとめることができる。

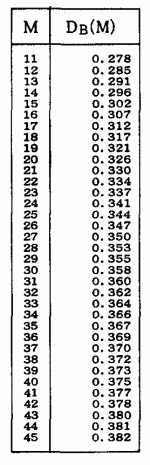
○差異係数D＝{SP両曲線の間にある1と0の数}÷{4×（受験者数）×（小問数）×（平均正答率）×（1−平均正答率）× 　ここで の整数部分を示し， は左の表からMに対応する をもとめることになる。

　差異係数Dの値は0.5前後が標準的であり，D＞0.6は要注意，D＜0.5のときは　Dが小さい程，指導と学習反時の密着性が高い。特に指導のステップの荒さ，発問，指示，目標の不明確さによって，Dの値は大となる。表3からDの値を求めてみる。SP両曲線の間の1と0の数は12，受験者数9人，小問数10 　しかし数表に10はないので11としてみる。 　平均正答率＝0.589

∴D＝12÷{4×9×10×0.589×（1−0.589）×0.278≒0.495密着性高い。

　<ア> 注意係数

　注意係数も分析，解釈には有効なはたらきをするが，くわしくは所報23号を参照していただきたい。

　-2-　学習推移表⇒児童の目標達成水準の理解の程度の変動を個々の児童ごとにおさえ，学習診断に活用するためのものである。

小問（S−P表）　段階

S−P表の児童の合計得点の平均点Mを中心に，合計得点の標準偏差бの半分をもってS−P表に区切り線をかき入れたものである。この区切りは一つの方法であって，別の区切り方をしてもさしつかえない。正規分布であれば段階3の範囲こ40%らの児童が含まれることになる。

　このようにして，毎授業後あるいは毎単元ごとに得られたS−P表に段階線をかきこみ個人ごとの変動をみる。

4．活用の実際

（1）全体傾向の把握

　・　平均正答率と得点，正答者数の分布状況について大づかみに全体の傾向を把握し，必要に応じ個々の数値をとりあげて検討する。

　・ SP両曲線の形から，テスト型，演習問題型，ドリル型，プログラム学習型のどのタイブにあたるかを判断していく。はじめドリルのつもりで与えたテストがテスト型的な反応であったということになれば，予想と実際には，かなりのズレがあったことになり検討が必要。

　・　指導を反省し，SP両曲線のズレの原因を検討する。ズレの大きさは，指導内容と児童の受けとり方との