福島県教育センター所報ふくしま　No.33（S52/1977.10） -013/026page

　図3

	（2）	用紙を2つに折り曲げ,軌道曲線が重さなったか確かめ,折り線と軌道の交点をＰＰ′とし,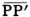 の中点をＣ（軌道の中心）,Ｃを通りＰＰ′に直交する軸ＱＱ′を引く。
	問1	火星軌道は円であるか,楕円であるか。 楕円の形（つぶれ具合）を示めすのに離心率ｅを用いる。 楕円の長半径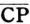 をａ,短半径 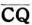をｂとすると 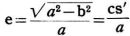　 で求められる。
	問2	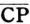（公転半径）の長さを天文単位で表わせ。
	問3	作図から火星軌道の離心率を求めよ。また,教科書の値と比較せよ。
	4　　ケプラーの第2法則の実習
目標
	ア	作図した火星軌道から,火星は一定の速さで運動していると言えるか。この事を調べるにはどのような方法で調べれぱよいか。
	イ	太陽と火星間の距離と速さ（火星が1日に動く角度）との関係を調べる。
実習II
	下の表の空欄に表IIのデータと火星軌道の作図から,それぞれの値を求めよ。
考察
	上の表より,太陽と火星の距離と速さとの間にどのような関係があるか。
実習III
	実習Iから遠日点付近では公転速度は小さく,近日点付近では公転速度が大きくなっていることがわかったが,量的に調べる方法はなかろうか。
	（1）	遠日点附近での△ＳＭ 7 Ｍ 8 の面積と近日点附近の△ＳＭ 4 Ｍ 5 　の面積を正方眼の数で求めよ。 （不完全な方眼は2つを1つとしてかぞえる)
	（2）	実習2で求めたθ,γの値を用いて,△ＳＭ 7 Ｍ 8 △ＳＭ 4 Ｍ 5 の面積から,動径が1日にえがく面積を求めよ。
考察
	1日に動経がえがく面積（速度面積）は,近日点附近と遠日点附近でどうか,また,他の場所ではどうか。
考察II
	考察Iより,面積速度はどこでも一定であると言えるか。
5　　ケプラーの第3法則の実習
目標
	太陽を中心とする惑星の公転運動や,地球の周りを廻わる月や人工衛星の公転運動において,公転半径と公転周期の間にどのような関係があるか探究し,また,ケプラーの第3法則が成り立つ事をデータから確かめる。
準備
	正方眼用紙　人工衛星資料　惑星の軌道資料
実習IV
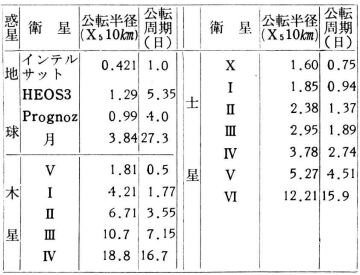
	正方眼紙を用いて,惑星の軌道資料（教科書）,表IIIのデータで各惑星の衛星の公転半径（横軸）と公転周期（縦軸）をプロットせよ。
表III
考察I
	公転半径と公転周期の間に何か規則性が発見できたかまた,各惑星の衛星はそれぞれ曲線上に並んでいる。それは何によるのか考えよう。
実習V

ア

ケプラーの第1法則の実習で求めた火星の公転半径と公転周期の値をケプラーの第3法則に代入せよ。