福島県教育センター所報ふくしま　No.33（S52/1977.10） -014/026page

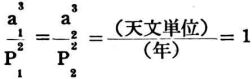
イ		他の惑星や人工衛星についても,ケプラーの第3法則が成り立つことを確かめよ。
留意点
	ケプラーの第3法則の指導は,データを式に代入して法則が成り立つことを確かめる方法が多くとられているが,探究を重視する立場から更に授業を発展させるのもよい。
	6　探究過程を重視したケプラーの第3法則の実習
目標
	公転運動とその中心にある天体の質量の関係をとらえ,ケプラーの第3法則を導く。
準備
	両対数方眼紙,惑星軌道の資料,表III　定規
実習VI
	両対数方眼紙を用いて,公転半径と公転周期の関係のグラフを作成する。
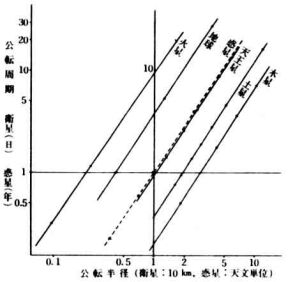
（1）		地球,木星,土星,天王星の衛星と,惑星の公転半径を両対数方眼紙の横軸に,公転周期を縦軸にとりプロットする。
		図4
（2）		プロットした点が,それぞれ一直線上に配列していることを確める。
（3）		地球から公転半径が10 5 kmの衛星（仮定）の公転周期を図4のグラフより読みとれ。
考察I
	図5より,公転半径γ,公転周期をＴとしたとき,両者の関係式を作れ。
実習VII
	公転半径を一定（1O 5 km）としたとき,質量と公転周期の間にどのような関があるか。
（1）		図4のグラフより,それぞれの惑星について公転半径が10 5 kmのときの衛星（仮定）の公転周期を読みとる。
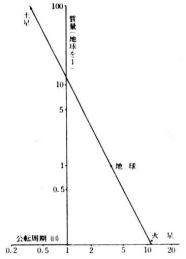
（2）		この公転周期の値を横軸に,それぞれの惑星の質量（地球の質量を1）を縦軸にとり,両対数グラフを作成せよ。
		図5
考察1
	図5のグラフより,公転周期をＴ,惑星の質量をＭとしたときのの両者の関係式を作れ。
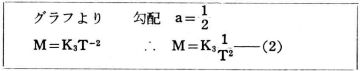
実習VIII
	公転周期を一定（3.7日）としたとき,質量と公転半径の間にどのような関係があるか。
（1）		図4のグラフから,各惑星の衛星の公転周期が3.7日となる公転半径を読みとる。
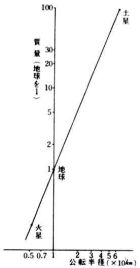
（2）		この公転半径の値を横軸に,それぞれの惑星の質量（地域を1）を縦軸にとり,両対数グラフを作成せよ。
		図6
考察I
	公転半径をγ,惑星の質量をＭとしたときの両者の関係の式を作れ。
考察II
	実習VII　VIIIより,質量,公転半径,公転周期の間にどのような関係がなりたつか。
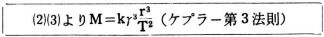