福島県教育センター所報ふくしま　No.43（S54/1979.10） -004/034page

　299，309，290の三つの数の大小関係を問う問題。
　2つの数なら簡単に大小関係が比較できるが，数が3つ4つと増加すると比較が困難になる。

（4）論理的思考力が未成熟であるためにつまずく。
　299，309，290の三つの数の中から最大の数をみつける。
　どの位の数字をくらべればよいかがつかめていない。

（5）心意的な発達の未熟さからくるつまずき。
　5＋40＝90　位取りの無視である。また，たし算の計算問題の中に，ひき算をまぜて出題するとひき算をたし算にしてしまう。

　中　学　年
（1）問題の表現の意味が受取りにくくてつまずく。
　3△53と△355の大小を比べる問題
　この種の問題を解いたことのない子どもには難解である。

（2）式と文章との交流がうまくできずつまずく。
　7×8＋7＝7×□，4＋8÷2，5＋4×6＋8，の計算で乗除先行の意味が完全に理解されていない。

（3）答えるために操作を必要とする場合につまずく。
　　　−本を読んだ人の人数−

曜日 学年	月	火	水	木	金	土
1　年	5	7	6	8	6	0
2　年	9	8	13	10	9	0
3　年	11	14	17	16	12	15
4　年	20	22	32	25	28	19
5　年	25	18	22	18	21	16
6　年	31	27	32	39	21	23

「本を読んだ人がいちばん多い曜日をしらべるには，どうすればよいですか。」の問に対するつまずきが多い。

（4）ことばで答えるときの表現の程度や形式になれないためにつまずく。
　だされた問題に対して，必要十分の条件を満たさない。よけいなことをいいすぎたり，必要なことをぬかす。

　高　学　年
（1）学習外の内容のためにつまずく。
　問題の内容がどの程度に新しい経験なのかを知っていないため。

（2）論理的になっていないためにつまずく。
　21÷6×7　＝　21÷7×6　＝　3×6＝18
　21は7で割れる誘惑に弱い。(21÷6)×7と21÷(6×7)の違いをよく理解していない。

（3）理解の混同によってつまずく。
　加滅法は小数をそろえて計算するため，これを，わり算にも使って誤る。

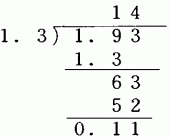
（4）ちがった連想がはいり込んでつまずく。

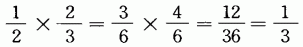
　分数のかけ算を通分して計算する。

（5）問題の一部分や推理の途中で反応するためにつまずく。

a	1　2　3　4　5
b	3　4　5　6　7

　aの値の変化だけをみてaとbは比例すると判断してしまう。

（6）思考が固定化するためにつまずく。

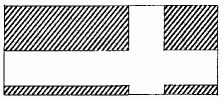
長方形の面積を求めることができても左図の斜線の部分の面積が求められない。

4　おわりに

　以上は，算数のつまずきについて，福島県標準学力診断検査問題などをもとに，類型化し，つまずきの具体的事例をあげ考察を加えたものである。