福島県教育センター所報ふくしま　No.53（S56/1981.10） -003/034page

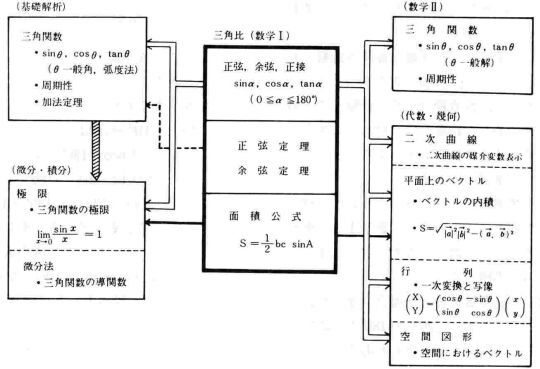
「三角比」と選釈科目との関連

応じて様々である。学習指導要領解説によれば，「教学1」の内容の取扱いは，「基本の趣旨は同じであるが」生徒に応じて「違っていても差し支えなく」場合によっては，「学習指導要領に示された内容について，先のことと関連の深いことなどを取り上げることがあってもよい」ことになっている。ただし，「学習指導要領の目標の趣旨や内容の範囲をはずれて，多くのことを指導することのないよう留意しなければならない」と述べられている。
　上の図は，「三角比の鈍角への拡張」を考える手がかりにしたいと思い，「三角比」と選訳科目との関連を示したものである。

　 4．三角比の鈍角への拡張（例）

　三角比の鈍角への拡張の方法は，一通りではない。有向線分を用いて定義する方法，座標を用いて定義する方法，それに三角形の辺や高さや面積を表す式の統一性から定義する方法などがある。
（1）有向線分を用いて定義する方法
　底辺を有向線分として考える。辺OA上の点Pから辺OBに垂線を下し，その足をQとする。この場合，∠POBが鋭角のときは，Qは辺OB上にあるが，∠POBが鈍角のときは，Qは辺OBの延長上にある。したがって，線分OQの向きが鋭角のときと逆になる。
　そこで，直線B′Bにおいて，OBの向きを正の向きとすると，鈍角の場合，OQは負の向きであるから， OQは，線分OQの長さに負の符号をつけたものを表す， と考える。

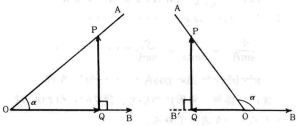
そして，∠POB＝αが鋭角の場合と同様に
　sinα＝QP/OP,　COSα＝OQ/OP，tanα＝QP/OQ
と定義する。
定義から，αが鋭角のとき　sinα＝sin（180度−α），cosα＝−COS（180度−α），tanα＝−tan（180度−α）
が導ける。
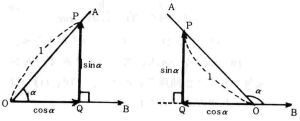
なお，OP＝1とした場合，すなわち点Pが点0から1だけOA上を進んだとき，水平方向の距離がcosαであり，鉛直方向の距離がsinαであることを付け加えておきたい。このことから，
sinO度＝0，cosO度＝1，sin90度＝1，cos90度＝0