福島県教育センター所報ふくしま　No.53（S56/1981.10） -004/034page

sin180度＝0，cos180度＝一1であることは，直観的に理解させることができよう。
　この方法は，前ページの下線の箇所の理解がむずかしいように思われる。直線に方向をつけるのは，すでに中学時代に，数直線の学習で経験しているが，負の符号で表した距離とは，初めての出会いであり，事前にその準備が必要となろう。
（2）座標を用いて定義する方法
　一般角の三角関数のときと同じように，座標を用いて定義する方法で，現行の「数学1」の教科書が，一般角の三角関数を定義するときに使っている方法なので省略する。
　「三角関数」への発展を考えた場合には，都合のよい方法だと思われる。三角比の180度までの拡張には，大げさではないかとの考えもある。
（3）三角形の辺や高さや面積を表す式の統一性から定義する方法
　　まず，鋭角三角形について
1　tanA＝sinＡ/cosＡ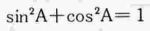， を導く。
2　S＝1/2bc sinA・・・・‥‥‥…‥‥‥………（ア）
　a/sinA＝b/sinB＝c/sinＣ・…‥………（イ）
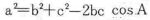　 　・‥・‥……（ウ）を導く。
　次に，鈍角三角形について，2の（ア）（イ）（ウ）に対応するものを考えてみる。
（ア）に対応するもの
　　　S＝1/2×ABXCH＝1/2bc sin（180度−A）・・・（ア）′
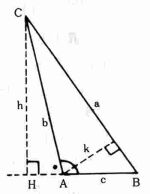（イ）に対応するもの
　sin（180度−A）＝h/b
　sinB＝h/a　より
　b sin（180度−A）＝a sinB
　∴a/sin（180度−A）＝b/sinＢ
　また，
　sinB＝k/c，sinＣ＝k/bより
　csinB＝bsinＣ　∴b/sinＢ＝c/sinＣ
　したがって
　a/sin（180度−A）＝b/sinＢ＝c/sinＣ……（イ）′
ここで，（ア）と（ア）′（イ）と（イ）′をくらべてみるとき，
sin（180度−A）がsinAに等しいとすれば，Aが鋭角であろうと鈍角であろうと，（ア）（ア）′，（イ）（イ）′はそれぞれ次の式で表される。
　　S＝1/2bc sinA，a/sinＡ＝b/sinＢ＝c/sinＣ
　　そこで，Aが鈍角のときsinA＝sin（180度−A）
　　と定義する。
（ウ）に対応するもの
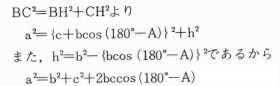　 　………・‥（ウ）′
（ウ）と（ウ）′とを比較するとき，もしcos（180度−A）が−cosAに等しければ，Aの大きさにかかわらず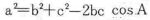， となる。
　そこで，Aが鈍角のときcosA＝−cos（180度−A）と定義する。
次に，Aが鈍角のときに，1　が成り立つようにしたい。
　sinＡ/cosＡ＝sin（180度−Ａ）/−cos（180度−A）＝−tan（180度−A）
　だから，tanA＝−tan（180度−A）と定義する。
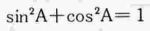　　 が成り立つことも示しておく。
　　この方法は，公式をより広い場面に適用できるように一般化していく過程がみれる利点がある。

　 5．おわりに

　どの方法で鈍角へ拡張するかは，生徒の実態，教師の教材観等によって異なると思われるが，今後検討を加え，さらに実際の指導のなかから，よりよい方法を見い出していきたいものである。
　ちなみに，昭和57年度用の「数学1」の教科書20冊を調べたところ，（1）の方法で記述しているのが7冊，（2）の方法が12冊，（3）が1冊であった。

　参考文献
学習指導要領　算数科数学科（試案）昭和22年　文部省
中学校数学指導書1959　文部省
高等学校学習指導要領解説（数学）1961，1972，昭和54年　文部省
教科書「数学1」各社
三角法　黒田孝郎　ダイヤモンド社
高等学校学習指導要領の展開（数学）田島一郎　福森信夫　明治図書
数学序説　吉田洋一　赤　攝也　培風館