福島県教育センター所報ふくしま　No.53（S56/1981.10） -031/034page

ア　長方形

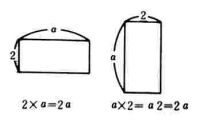
イ．長方形

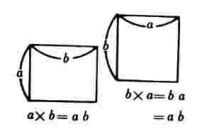
ウ．長方形　　エ．長方形

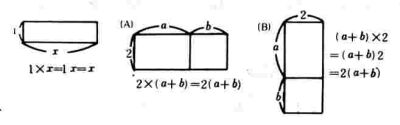
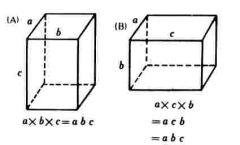
オ．直方体

カ．正方形

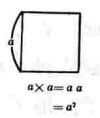
キ．立方体

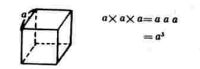
2　図を見て面積や体積の式を作らせると上記のように立式する。
3　面積や体積図を用いてその積を求めさせる中で文字式の乗法のきまりを考えていく。
　ア．式や計算はできるだけ単純化する方向で表現するのがよいから乗法記号を省略する‥・（1）
　イ．長方形の図（A）と（B）や直方体の図（A）と（B）を比較検討させると

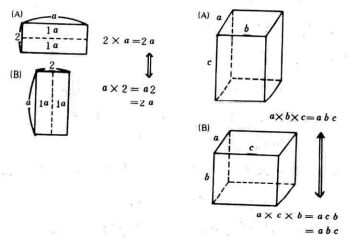
（A），（B）とも面積や体積が同じことから，面積や体積の値の表現を統一する必要性を感じさせ，生徒との話し合いの中で，乗法のきまり
　○数×文字では数が前……（2）
　○文字の乗法では，文字はアルファベット順にならべる・・・…（3）
という乗法のきまりが生徒に理解させることができる。
　ウ. 1×x＝1x＝x‥・…（4）
　エ．正方形の面積

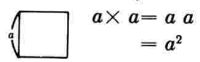
　オ．立方体の体積

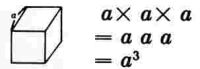
　　（注）数の累乗の表し方は正負の数の計算でやっている。
　というように，文字式の乗法のきまりが無理なく指導できる。
4．実践の結果
　このように実践してみて指導の結果を反省するために事後テストを実施して分析してみた。
（調査対象生徒数　34名）

計算	b×a	a×3	（x-y）×2	x×ｃ×3	1×ｘ
正答数	31/34	33/34	29/34	32/34	33/34
主な誤答例	ba	a3	2xy	3xc	1x

〔考察〕1　文字式の乗法のきまりもだいたい理解されたと思うが完全ではない。
　　　2　演算記号×と演算記号＋，−の扱い方の区別をもっと明確に指導すべきであった。（＋，−を省略した生徒がいた。）
5．反省と考察 　
　（1）反省
　1　面積図や体積図を用いて文字使用のきまりを指導すると抽象的なきまりが具体的に理解させることができる。
　2　比較的学力の遅れている生徒でも意欲をもって学習に取り組むようになるし，上位の生徒も進んだ問題（例　4x×5，15×（−a））にも積極的に取り組むようになる。
　3　普通より指導時数が余計にかかるが次の商の表し方の指導や文字式の計算の定着もよい。
（2）考察　
　1　面積図はさらにいろいろの文字式の計算の意味づけに有効に使える。

1年　文字使用のきまり→同類項をまとめる→1次式の加減

　　↓

2年　単項式乗除→多項式の加減→単項式と多項式の乗除

　　↓

3年　多項式の乗法→多項式の乗法公式