福島県教育センター所報ふくしま　No.61（S58/1983.06） -026/042page

アイディア紹介

数学科における単元の統合化を考えた教材の開発

郡山市立郡山第三中学校　原田　伊佐雄

1　はじめに
　数学の指導において，特に，基礎的・基本的事項の指導に重点がおかれている。そのため，教材間の統合的な見方，さらにはその融合化を図るような教材の開発が少なかったように思われる。

　それぞれの教材が別々にあるのではなく，教材相互の関連を考え，いくつかの教材を統合化した指導内容を工夫することによって，数学科の目標の達成にせまることができるのではないかと考えた。　ここでは，関数教材と図形教材（相似形の相似比面積比）を例として述べる。

２　教材の統合化
　関数の代表形であるy＝aX，y＝aX＋b，yニaX字の式が相似形を変化（拡大）させるとき，周の長さ，面積比，面積の差のなかにみごとに存在している。

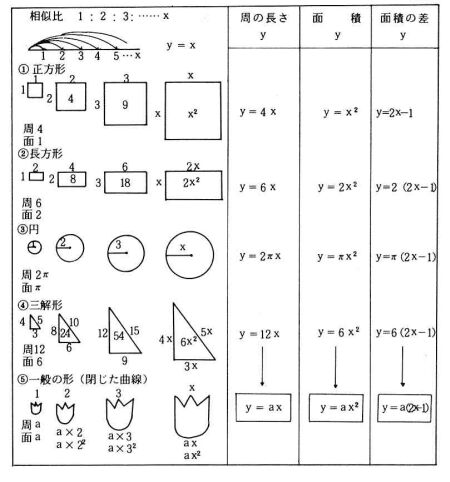
　図形の拡大からできる相似比を「変化」ととらえ，相似比をもとにして，相似形の周の長さ，面積，面積の差へと「対応」させる。その操作が関数的な見方や考え方を育てるとともに，その発展性も明確にしてくれる。そして，相似比一面積比一体積比との関係をより深く理解させることになる。

３　実践例
（１）　指導内容と時間　（18）
　1　いろいろな関数　　10
　2　集合と関数　　　　6
　・関数の考え方から相似な　図形を考察する（本時5／6）
　3　まとめと評価　　　2

（２）本時のねらい
相似形の拡大と関数の考え方を統合的にみることによって，数学的な表現や処理する能力を高める。

（４）　課題の提示と解決についての考察
　正方形を整数倍に拡大するときの相似比と周，面積，面積の差の変化について関数関係を見つけていくように設定した。

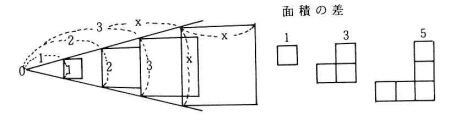
・正方形の拡大図が，同じ形に作図できるように，　プリントに相似の中心や基本線は準備しておいた。
・相似比を変数とみて，Ⅹ倍する考え方は，スムー　ズに理解した。連続量であることにも軽くふれた。
・拡大される正方形の何に着目して，相似比を対応　するかポイントである。生徒は周や面積について　は，見つけてくれた。しかし，面積の差は，図示　しながらこちらで指摘した。
・面積の差の1次関数の式づくりは，奇数の集合で　あることから考えた生徒が多かった。

４　おわりに
　数学は，下から上へ整然と積み上げられている学問である。それ故，基礎的・基本的な内容を確実に定着させることは，一番の課題である。また，教材相互の関連を図る指導のくふうは，生徒の学習意欲，興味，関心を高め，自ら探究する態度を養うためにも極めて重要なことであると考える。

掲載情報の著作権は情報提供者及び福島県教育センターに帰属します。