福島県教育センター所報ふくしま　No.70（S60/1985.2） -004/042page

ここが等しく,平行だよ。」
P1「この図は,2つの三角形がきっと合同だよ。合同ならOAとODは等しくなるから。」
P2「そうだな。本当に合同かどうかわからないがもし合同なら,結論が成り立つね。合同になることを言えばいいんだ。」
P1「そうすると,ABとCDは等しい。この角は対頂角だから等しい(∠AOB=∠DOC)。AOとODも等しいぞ。」
P2「そこは赤色で結論だから使ってだめだよ。」
P2「この角とこの角は同じだ。」
P1「どうしてだい。」
P2「だって,こことここが平行だから錯角になっている角は等しいから。」
P1「それじゃ∠Bと∠Cも等しい」
P2「そうすると合同条件のどれかな。」
P2「まず,3辺による合同はだめ。等しい辺はこことここだから……」
P1「わかった。1辺と両端の角だよ。」
P2「じゃ,整理してまとめるよ。」

　ここで,話し言葉に近いものでよいから,ノートに簡単に証明をメモさせることもよいと思われる。T「じぁ,発表してもらいます。じぁP2君。」

P2の発表例(黒板の前で図を見ながら) 「この2つの三角形が合同ならば,こことここは等しくなります。2つの三角形は,1辺と両端の角がそれぞれ等しいので合同になります。それは,こことここが等しく,この角とこの角,あと,この角とこの角が等しいからです。だから,合同になったから等しいです。」

P3「∠Aと∠D,∠Bと∠Cが"平行線の錯角"で等しいと理由を言った方がいいと思います。」
P4「P2君の証明は正しいのですが,こことこことか,この角とこの角のような言い方でなく,せっかく図に記号がついているのだから,その記号を使って言った方がよいと思います。」

　生徒の発表をそのままの表現で板書し,どう述べればわかりやすいか,または,P4のような指摘はなぜ大切なのかについて話し合わせる。

T「それでは,この証明がどんな図形の基本性質を使って成り立っているのか,そのしくみを図示してみましょう。」

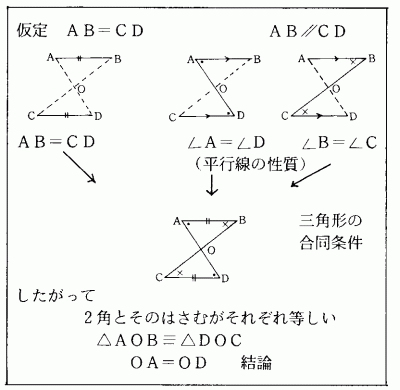
上のように証明のしくみを図示することにより合同条件を適用した推論の過程が明確になり,証明を簡単にわかりやすく表現するには,どのような順序で表現することがよいか明らかになる。口頭で述べさせる指導の留意点は,最初は話し言葉に近いもので,図を指し示しながら,推論の筋道を正しく言えるようにする。次に図の記号などを用いて,「この三角形AOBとこの三角形DOCにおいて」のような数学らしい表現をさせ,証明の形を整えていくように指導する。

　以上述べたように,第二,三段階において,論証する能カを育てておけば,次の第四段階の証明の記述では,生徒が自信を持って学習にとりくみ,証明を書くという表現能カが高まるものと考えられる。

4.おわりに

証明問題ができたときの喜びは,格別のものがあるような気がする。そんな気持ちをひとりでも多くの生徒に味わいさせたいと思う。それには,生徒が自ら考えて証明をしようとするような魅カある証明指導をしていかねばならないと考える。今後,生徒の学習意欲を高め,証明する能カを一層伸ばすような指導法の工夫・改善が望まれるところである。

参考文献

中学校指導書数学編	文部省
教材研究のすすめ	佐藤俊太郎 　明治図書
図形とその指導	日本数学教育会編　 明治図書
図形と論理	石谷茂 　　　啓林館